Tag: rotating flow

Jupiter in a Lab
The vivid bands of a gas giant like Jupiter come from the planet’s combination of rotation and convection. It’s possible to create the same effect in a lab by rapidly spinning a tank of water around a central ice core. That’s the physical set-up behind this research poster–note the illustration in the lower right corner. The central snapshots show how temperature gradients on the water surface change the faster the tank rotates. At higher rotational speeds, the parabolic water surface gets ever steeper and Jupiter-like temperature bands form. (Image credit: C. David et al.)
Fediverse Reactions
January 28, 2026
Event-Based Recording
High-speed cameras are an amazing tool in fluid dynamics, but they come with a whole host of challenges. The camera and lighting have to be positioned to deal with reflections, the data sets are enormous, and post-processing all that data takes a long time.
Here, researchers experiment instead with studying a flow using an event-based camera, which records information only when and where the brightness changes. The images and videos look strange to our eyes, but, as the authors show, they work nicely for identifying flow features and extracting valuable data. (Video and image credit: D. Sun et al.)
Fediverse Reactions
January 5, 2026
Competing Time Scales
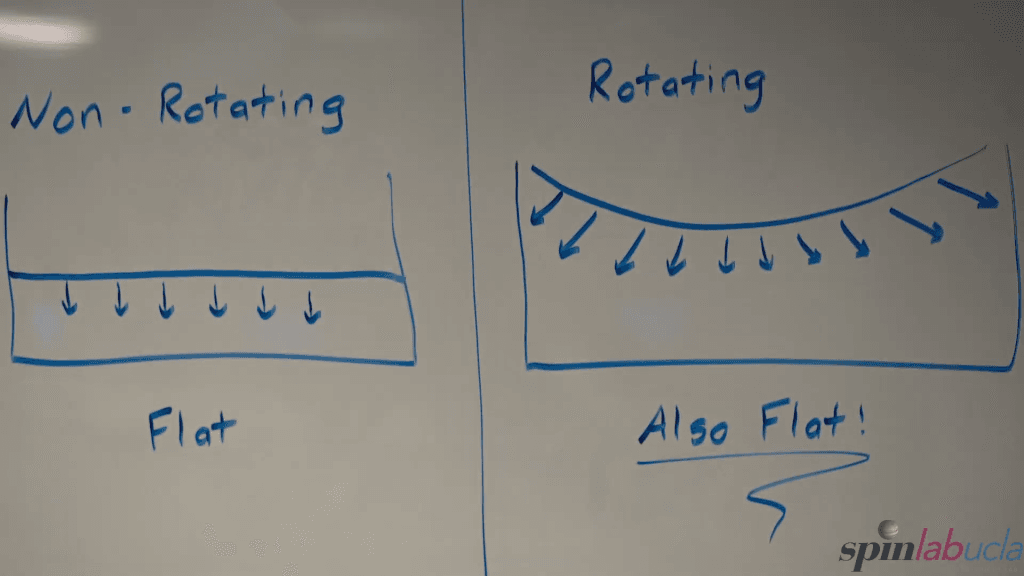
Fluid dynamics often comes down to a competition between the different forces acting in a flow. Inertia, surface tension, viscosity, gravity, rotation — flows can be affected by all of these and more. In this video, researchers describe the three dominant forces in a rotating fluid like a planet’s atmosphere: viscosity, the fluid’s resistance to flowing; inertia, the fluid’s resistance to accelerating; and rotation, the overall spin of a fluid.
As shown in the video, which of these three forces dominates will change depending on the speed at which the force acts. We quantify this concept using time scales; the force with the smallest time scale can act fastest and will, therefore, win the tug-of-war. (Video and image credit: UCLA SpinLab)
Fediverse Reactions
November 10, 2025
Spinning Water
If you spin a tank of water at a constant speed, it takes on a curved, parabolic shape–a demonstration often called Newton’s bucket. Here, a team from UCLA shows how it’s done, both in terms of the equipment needed and a concise explanation of the physics. In the rotating experiment, water is subjected to both gravity (which acts in a constant magnitude across the tank) and centrifugal force (which is stronger further from the axis of rotation). The shape that balances these forces is a paraboloid, which is why the water takes on that shape. (Video and image credit: UCLA SpinLab)
Fediverse Reactions
September 29, 2025
Bubbly Tornadoes Aspin
Rotating flows are full of delightful surprises. Here, the folks at the UCLA SpinLab demonstrate the power a little buoyancy has to liven up a flow. Their backdrop is a spinning tank of water; it’s been spinning long enough that it’s in what’s known as solid body rotation, meaning that the water in the tank moves as if it’s one big spinning object. To demonstrate this, they drop some plastic tracers into the water. These just drop to the floor of the tank without fluttering, showing that there’s no swirling going on in the tank. Then they add Alka-Seltzer tablets.
As the tablets dissolve, they release a stream of bubbles, which, thank to buoyancy, rise. As the bubbles rise, they drag the surrounding water with them. That motion, in turn, pulls water in from the surroundings to replace what’s moving upward. That incoming water has trace amounts of vorticity (largely due to the influence of friction near the tank’s bottom). As that vorticity moves inward, it speeds up to conserve angular momentum. This is, as the video notes, the same as a figure skater’s spin speeding up when she pulls in her arms. The result: a beautiful, spiraling bubble-filled vortex. (Video and image credit: UCLA SpinLab)
Fediverse Reactions
February 24, 2025
The Best of FYFD 2024
Welcome to another year and another look back at FYFD’s most popular posts. (You can find previous editions, too, for 2023, 2022, 2021, 2020, 2019, 2018, 2017, 2016, 2015, and 2014. Whew, that’s a lot!) Here are some of 2024’s most popular topics:
This year’s topics are a good mix: fundamental research, civil engineering applications, geophysics, astrophysics, art, and one good old-fashioned brain teaser. Interested in what 2025 will hold? There are lots of ways to follow along so that you don’t miss a post.
And if you enjoy FYFD, please remember that it’s a reader-supported website. I don’t run ads, and it’s been years since my last sponsored post. You can help support the site by becoming a patron, buying some merch, or simply by sharing on social media. And if you find yourself struggling to remember to check the website, remember you can get FYFD in your inbox every two weeks with our newsletter. Happy New Year!
(Image credits: dam – Practical Engineering, ants – C. Chen et al., supernova – NOIRLab, sprinkler – K. Wang et al., wave tank – L-P. Euvé et al., “Dew Point” – L. Clark, paint – M. Huisman et al., iceberg – D. Fox, flame trough – S. Mould, sign – B. Willen, comet – S. Li, light pillars – N. Liao, chair – MIT News, Faraday instability – G. Louis et al., prominence – A. Vanoni)
Fediverse Reactions
January 1, 2025
How Magnetic Fields Shape Core Flows
The Earth’s inner core is a hot, solid iron-rich alloy surrounded by a cooler, liquid outer core. The convection and rotation in this outer core creates our magnetic fields, but those magnetic fields can, in turn, affect the liquid metal flowing inside the Earth. Most of our models for these planetary flows are simplified — dropping this feedback where the flow-induced magnetic field affects the flow.
The simplification used, the Taylor-Proudman theorem, assumes that in a rotating flow, the flow won’t cross certain boundaries. (To see this in action, check out this Taylor column video.) The trouble is, our measurements of the Earth’s actual interior flows don’t obey the theorem. Instead, they show flows crossing that imaginary boundary.
To explore this problem, researchers built a “Little Earth Experiment” that placed a rotating tank (representing the Earth’s inner and outer core) filled with a transparent, magnetically-active fluid inside a giant magnetic. This setup allowed researchers to demonstrate that, in planetary-like flows, the magnetic field can create flow across the Taylor-Proudman boundary. (Image credit: C. Finley et al.; research credit: A. Pothérat et al.; via APS Physics)
November 21, 2024
Trapped in a Taylor Column
The world’s largest iceberg, A23a, is stuck. It’s not beached; there are a thousand meters or more of water beneath it. But thanks to a quirk of the Earth’s rotation, combined with underwater topology, A23a is stuck in place, spinning slowly for the foreseeable future. A23a is trapped in what’s known as a Taylor column, a rotating column of fluid that forms above submerged objects in a rotating flow. You can see the same dynamics in a simple tabletop tank.
Pirie Bank sticks up from the seafloor, which sets up a stationary column of rotating water that iceberg A23a is now stuck in.
When a tank (or planet) is rotating steadily, there’s little variation in flow with depth. With an obstacle at the deepest layer — in this case, an underwater rise known as the Pirie Bank — water cannot pass through that lowest layer. And that deflection extends to all the layers above. The water above Pirie Bank just stays there, as if the entire column is an independent object. Caught inside this region, A23a will remain imprisoned there. How long will that last? There’s no way to know for sure, but a scientific buoy in another nearby Taylor column has been hanging out there for 4 years and counting. (Image credit: A23a – D. Fox/BAS, diagram – IBSCO/NASA; via BBC News; submitted by Anne R.)
August 21, 2024
Stopping a Bottle’s Bounce
A few years ago, the Internet was abuzz with water bottle flips. Experimentalists are still looking at how they can arrest a partially fluid-filled container’s bounce, but now they’re rotating the bottles vertically rather than flipping them end-over-end. Their work shows that faster rotating bottles have little to no bounce after impacting a surface.
This image sequence shows how water in a rotating bottle moves during its fall (top row) and after impact (bottom row). Water climbs the walls during the fall, creating a shell of fluid that, after impact, forms a central jet that arrests the bottle’s momentum.
The reason for this is visible in the image sequence above, which shows a falling bottle (top row) and the aftermath of its impact (bottom row). When the bottle rotates and falls, water climbs up the sides of the bottle, forming a shell. On impact, the water collapses, forming a central jet that shoots up the middle of the bottle, expending momentum that would otherwise go into a bounce. It’s a bit like the water is stomping the landing.
The authors hope their observations will be useful in fluid transport, but they also note that this bit of physics is easily recreated at home with a partially-filled water bottle. (Image and research credit: K. Andrade et al.; via APS Physics)
September 28, 2023
Spinning Liquids With Lego
One way to explore the effects of spinning liquids at high-speeds is to build an expensive and precise lab apparatus. Another method is to raid the Lego bin. Here, a YouTuber builds ever-more-elaborate Lego constructions to spin a sphere of water. He begins with a relatively straightforward magnetic stirrer that creates a bathtub vortex in his sphere, but as the set-up grows, he eventually encases the sphere to spin the entire thing at high-speed. It’s a cool way to see how spinning liquids react, from forming a vortex to spin coating the interior of the sphere and to generating a parabolic interface between air and liquid. Set-ups like these are not merely for fun, though; scientists use them to simulate the interiors of planets. (Image and video credit: Brick Technology; submitted by clogwog)
January 23, 2023