Computational fluid dynamics and supercomputers can produce some stunning flow visualizations. Above are examples of turbulence, the Rayleigh-Taylor instability, and the Kelvin-Helmholtz instability. Be sure to check out LCSE’s website for more; they’ve included wallpapers of some of the most spectacular ones. (Photo credits: Laboratory for Computational Science and Engineering, University of Minnesota, #)
Tag: Rayleigh-Taylor instability

Fractal Fluids
Part of the beauty of numerical simulation is its ability to explore the physics of a situation that would difficult or impossible to create experimentally. Here the Rayleigh-Taylor instability–which occurs when a heavier fluid sits atop a lighter fluid–is simulated in two-dimensions. Viscosity and diffusion are set extremely low in the simulation; this is why we see intricate fractal-like structures at many scales rather than the simulation quickly fading into gray. (The low diffusion is also what causes the numerical instabilities in the last couple seconds of video.) The final result is both physics and art. (Video credit: Mark Stock)

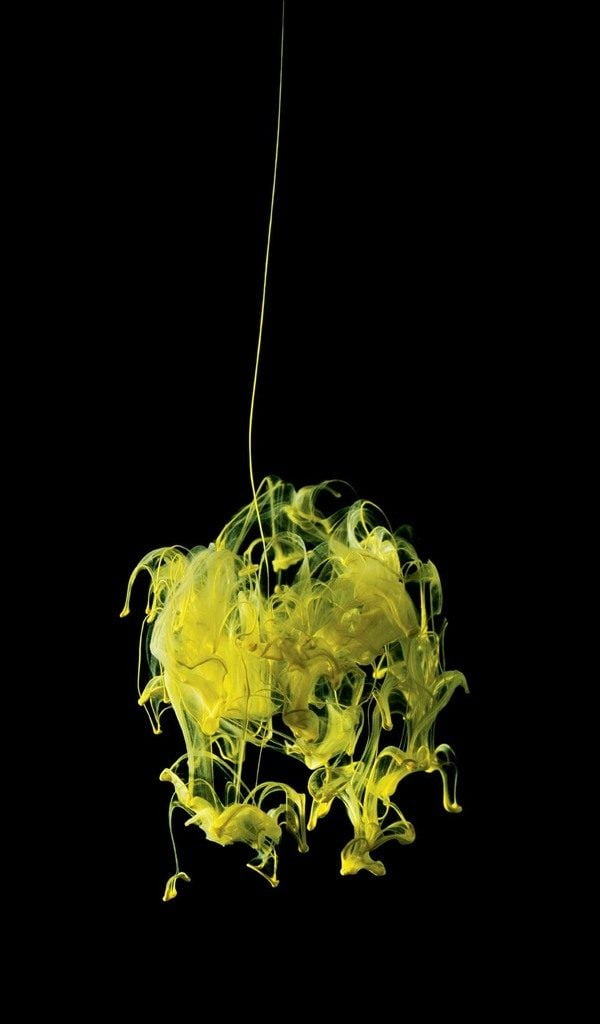
Ink Sculptures
Dripping ink into water can create fantastic structures as the two fluids mix. In this artwork there are numerous complex mixing phenomena: the eddies and multiple scales of turbulence; the long, thin streams of laminar flow; and the wispy mushrooms and umbrellas of the Rayleigh-Taylor instability. (Photo credit: Mark Mawson; via @thinkgeek)
Water Balloon Physics
[original media no longer available]
This video explores some of the physics behind the much-loved bursting water balloon. The first sections show some “canonical” cases–dropping water balloons onto a flat rigid surface. In some cases the balloon will bounce and in others it breaks. The bursting water balloons develop strong capillary waves (like ripples) across the upper surface and have some shear-induced deformation of the water surface as the rubber peals away. Then the authors placed a water balloon underwater and vibrated it before bursting it with a pin. They note that the breakdown of the interface between the balloon water and surrounding water shows evidence of Rayleigh-Taylor and Richtmyer-Meshkov instabilities. The Rayleigh-Taylor instability is the mushroom-like formation observed when stratified fluids of differing densities mix, while the Richtmyer-Meshkov instability is associated with the impulsive acceleration of fluids of differing density.

High-Res Rayleigh-Taylor Instability
When a heavy fluid sits atop a lighter fluid, the interface between the two breaks down through the Rayleigh-Taylor instability. This computation of a 2D interface shows the near fractal behavior of this instability as whorls and eddies of all different scales form and mix the fluids. (submitted by @markjstock)

Rayleigh-Taylor Art
The Rayleigh-Taylor instability occurs when a denser fluid lies atop a lighter fluid (relative to the gravitational field). The interface between the fluids deforms and the two fluids form finger-like protrusions that turn into mushroom caps and mix the dissimilar fluids together. This video, though based on a 2D Rayleigh-Taylor instability numerical simulation, was actually part of an art exhibit. (submitted by Mark S)
Personally, I recommend putting together a playlist of your favorite late 60s/early 70s rock (Pink Floyd, late Beatles, Jimi Hendrix, etc.) and sticking it on in the background while you watch the video in HD. It’s totally worth the 15 minutes. Especially in the later stages of each segment, the mixing between fluid layers really brings to mind cloud patterns on Jupiter or Saturn.

Jet Breakup
A non-cylindrical stream falling through a slit nozzle exhibits the Plateau-Rayleigh instability, which drives a falling jet of fluid to break into droplets due to surface tension. The fingers formed off the falling stream may be a form of Rayleigh-Taylor instability. #

Upside-Down Umbrellas
When a heavier fluid is suspended over a lighter fluid (as with ink or food coloring in water), the interface between fluids is subject to the Rayleigh-Taylor instability. As the heavier fluid starts to sink, it forms “fingers”, which develop into mushroom-cap shapes as the fluid continues falling. Sometimes the shear stress between the heavier fluid and lighter fluid causes secondary Kelvin-Helmholtz instabilities as well. (Photo by Leonardo Aguiar)

Oil Chandeliers
What you see above is a composite of images of an oil droplet falling into alcohol from two different heights. The top row of images is from a height of 25 mm and the bottom from a height of 50 mm. The first droplet forms an expanding vortex ring which breaks down via the Rayleigh-Taylor instability due to its greater density than the surrounding alcohol. The second droplet impacts the alcohol with greater momentum and is initially deformed by viscous shear forces. Eventually it, too, breaks down by the Rayleigh-Taylor mechanism. This image is part of the 2010 Gallery of Fluid Motion. # (PDF)
Effects of Viscosity
[original media no longer available]
Today’s video demonstrates the effect of viscosity, which measures a fluid’s resistance to deformation. On the left is a column of highly viscous fluid; the fluids become less viscous as one moves right. When a jet of dye is released into the highly viscous fluid, the jet is very slow to penetrate, whereas, in the rightmost column, the dye expands quickly into a turbulent jet. Between these extremes, we see a laminar dye jet entering the liquid. The mushroom-like shape the laminar jet takes is the result of the Rayleigh-Taylor instability, which occurs when a denser fluid is on top of a lighter fluid in a gravitational field.