FYFD

Tag: viscosity

  • Featured Video Play Icon

    Competing Time Scales

    Fluid dynamics often comes down to a competition between the different forces acting in a flow. Inertia, surface tension, viscosity, gravity, rotation — flows can be affected by all of these and more. In this video, researchers describe the three dominant forces in a rotating fluid like a planet’s atmosphere: viscosity, the fluid’s resistance to flowing; inertia, the fluid’s resistance to accelerating; and rotation, the overall spin of a fluid.

    As shown in the video, which of these three forces dominates will change depending on the speed at which the force acts. We quantify this concept using time scales; the force with the smallest time scale can act fastest and will, therefore, win the tug-of-war. (Video and image credit: UCLA SpinLab)

    Fediverse Reactions
  • Venusian Gravity Currents

    Venusian Gravity Currents

    Radar measurements of Venus‘s surface reveal the remains of many volcanic eruptions. One type of feature, known as a pancake dome, has a very flat top and steep sides; one dome, Narina Tholus, is over 140 kilometers wide. Since their discovery, scientists have been puzzling out how such domes could form. A recent study suggests that the Venusian surface’s elasticity plays a role.

    According to current models, the pancake domes are gravity currents (like a cold draft under your door, an avalanche, or the Boston Molasses Flood), albeit ones so viscous that they may require hundreds of thousands of Earth-years to settle. Researchers found that their simulated pancake domes best matched measurements from Venus when the lava was about 2.5 times denser than water and flowed over a flexible crust.

    We might have more data to support (or refute) the study’s conclusions soon, but only if NASA’s VERITAS mission to Venus is not cancelled. (Image credit: NASA; research credit: M. Borelli et al.; via Gizmodo)

    Fediverse Reactions
  • A New Mantle Viscosity Shift

    A New Mantle Viscosity Shift

    The rough picture of Earth’s interior — a crust, mantle, and core — is well-known, but the details of its inner structure are more difficult to pin down. A recent study analyzed seismic wave data with a machine learning algorithm to identify regions of the mantle where waves slowed down. These shifts in seismic wave speed occur in areas where the mantle’s viscosity changes; a higher viscosity makes waves travel slower.

    The team found seismic wave speed shifts at depths of 400 and 650 kilometers, corresponding to known viscosity changes. But they found shifts at 1050 and 1500 kilometers, as well — the first time anyone has shown a global viscosity shift at those depths. Their analysis suggests a higher viscosity in this mid-mantle transition zone, which could affect how tectonic plates, which rely on these slow mantle flows, move. (Image credit: NASA; research credit: K. O’Farrell and Y. Wang; via Eos)

  • Featured Video Play Icon

    Marangoni Blossoms

    When surface tension varies along an interface, fluids move from regions of low surface tension to higher surface tension, a behavior known as the Marangoni effect. Here, a drop of (dyed) water is placed on glycerol. The two fluids are miscible, but water has much a lower viscosity and density yet a higher surface tension. The drop’s interface quickly becomes unstable; viscous fingers form along the edge as the less viscous water pushes into the more viscous glycerol. Eventually, the surface-tension-driven Marangoni flow breaks those fingers off into lip-like daughter drops. The researchers also show how the interplay between viscosity and surface tension affects the size of fingers that form by varying the water/glycerol concentration. (Image and video credit: A. Hooshanginejad et al.)

  • Saving Screens with Shear-Thinning Fluids

    Saving Screens with Shear-Thinning Fluids

    These days glass screens travel with us everywhere, and they can take some big hits on the way. Manufacturers have made tougher glass, but they continue to look for ways to protect our screens. Recently, a study suggested that non-Newtonian fluids are well-suited to the task.

    The team explored the physics of sandwiching a layer of fluid between a glass top layer and an LCD screen bottom layer, mimicking structures found in electronic devices. Through simulation, they searched for the fluid characteristics that would best minimize the forces felt by the solid layers during an impact. They found that shear-thinning fluids — fluids that, like paint or shampoo, get runnier when they’re deformed — provided the best protection. Having the impact energy go into reducing the local viscosity of the fluid stretches the length of time the impact affects the glass, which lowers the bending forces on it and helps avoid breakage. (Image credit: G. Rosenke; research credit: J. Richards et al.; via Physics World)

  • Evolving Fingers

    Evolving Fingers

    If you sandwich a viscous fluid between two plates and inject a less viscous fluid, you’ll get viscous fingers that spread and split as they grow. This research poster depicts that situation with a slight twist: the viscous fluid (transparent in the image) is shear-thinning. That means its viscosity drops when it’s deformed. In this situation, the fingers formed by the injected (blue) fluid start out the way we’d expect: splitting as they grow (inner portion of the composite image). But then, the tip-splitting stops and the fingers instead elongate into spikes (middle ring). Eventually, as the outer fluid’s viscosity drops further, the fingers round out and spread without splitting (outer arc of the image). (Image credit: E. Dakov et al.; via GoSM)

  • Weathering Spilled Oil

    Weathering Spilled Oil

    As long as we continue to extract and transport oil, marine oil spills will continue to be a problem. Recent work shows that spilled oil weathers differently depending on both sunlight and water temperature. When exposed to sunlight, crude oil undergoes chemical reactions that can change its makeup. Researchers studied the mechanical properties of crude oil samples kept at different temperatures in both sunlight and the dark.

    They discovered that sunlight-exposed crude oil kept at a high temperature had twice the viscosity of a sample kept in the dark at the same temperature. In contrast, the high-temperature sunlit sample’s viscosity was 8 times lower than a sunlit sample kept at a lower temperature. That’s quite a large difference, and it implies that tropical oil spills may behave quite differently than Arctic ones. Cold-water spills will entrain and dissolve less than warm-water ones, so there may be more surface oil to collect at high-latitude spills. The differences in viscosity may also necessitate different spill mitigation techniques. (Image credit: NOAA; research credit: D. Freeman et al.; via APS Physics)

  • Featured Video Play Icon

    Can Water Solve a Maze?

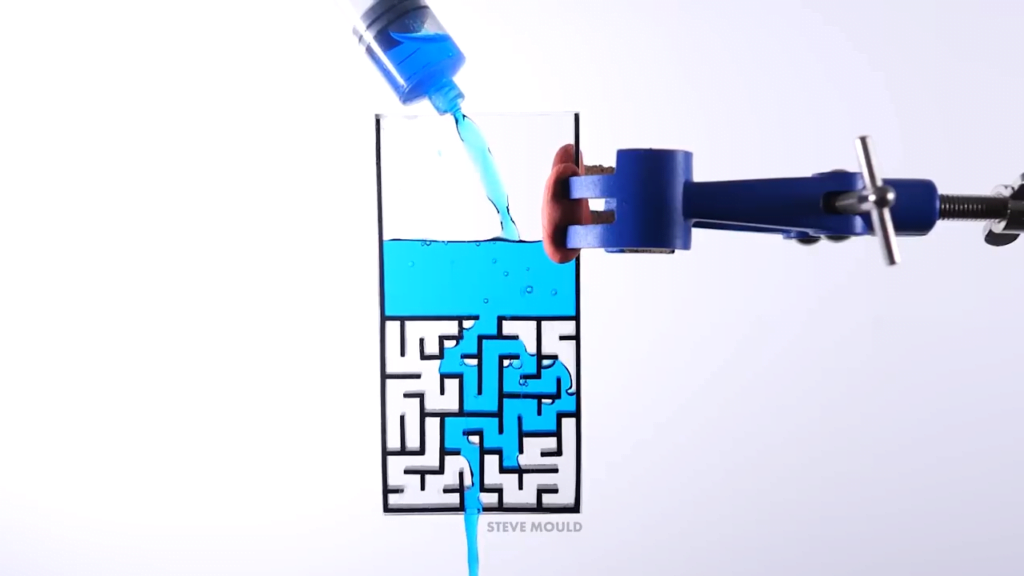
    Inspired by a simulation, Steve Mould asks a great question in this video: can water solve a maze? Yes — with some caveats. Steve makes two different maze patterns — a simple and a complex path — in two different sizes. With the small, simple-path version, the water immediately follows the correct path without taking any wrong turns. What keeps it on the right path seems to be a combination of air pressure and surface tension. In the dead-end passages, the air has nowhere to go in order to allow the water in. So the pressure of the trapped air and the narrowness of the passages (which allows surface tension to help hold the water in place) keeps the water out of the false paths.

    With the larger mazes, the water is able to take some false turns as it seeks the lowest possible path. But after awhile the incorrect region fills and the water takes the next lowest path available, which eventually leads it to the outlet.

    Toward the end of the video, Steve notes that the large mazes sometimes stop flowing, even though water is still in the reservoir. I’ll quibble slightly here with his explanation, though; I don’t think surface tension is playing as much of a role in this stoppage as friction. The water is basically being driven through a long, narrow pipe, which means quite a lot of friction between it and the walls. Just as you need a certain driving pressure to keep water in a pipe flowing, the maze needs a high enough driving pressure to keep the water going. The point at which drainage stops is the point where the upstream pressure (caused by the depth of the reservoir above the maze) is equal to the pressure lost due to friction in the pipe. All in all, it’s a very cool experiment and a video well-worth watching! (Video and image credit: S. Mould)

  • Finger Painting Physics

    Finger Painting Physics

    Spreading paint with a brush or with fingers is familiar activity for most people. It’s also similar to processes used in industry for spreading thin layers of paint and other complex fluids. In a recent study, researchers took a look at how a soft, elastic blade (similar to a paintbrush or one’s fingers) spreads shear-thinning fluids (like paint) and Newtonian fluids (like water). Surprisingly, they found that it actually takes 30% more mechanical work to spread a shear-thinning fluid than the same volume of an equivalent Newtonian one. That’s pretty much the opposite of what we’d expect since the action of spreading (and shearing) the complex fluid should reduce its viscosity. However, they did find that the shear-thinning fluid spreads to a thin layer more consistently than the Newtonian fluid does. (Image credit: A. Kolosyuk; research credit: M. Krapez et al.)

  • Bubbles in Turbulence

    Bubbles in Turbulence

    In nature and industry, swarms of bubbles* often encounter turbulence in their surrounding fluid. To study this situation, researchers used numerical simulation to observe bubbles across a range of density, viscosity, and surface tension values relative to their surroundings. They found that density differences between the two fluids made negligible changes to the way bubbles broke or coalesced.

    In contrast, viscosity played a much larger role. More viscous bubbles were less likely to deform and break, thanks to their increased rigidity. When looking at small deformations along the bubble interface, both density and viscosity had noticeable effects. With increasing bubble density, they observed more dimples on the interface; increasing the viscosity had the opposite effect, making the bubbles smoother. (Image credit: Z. Borojevic; research credit: F. Mangani et al.)

    *We usually think of bubbles as air or another gas contained within a liquid. But this study’s authors use the term “bubble” more broadly to mean any coherent bits of fluid in a different surrounding fluid. Colloquially, this means their results apply to both bubbles and drops.