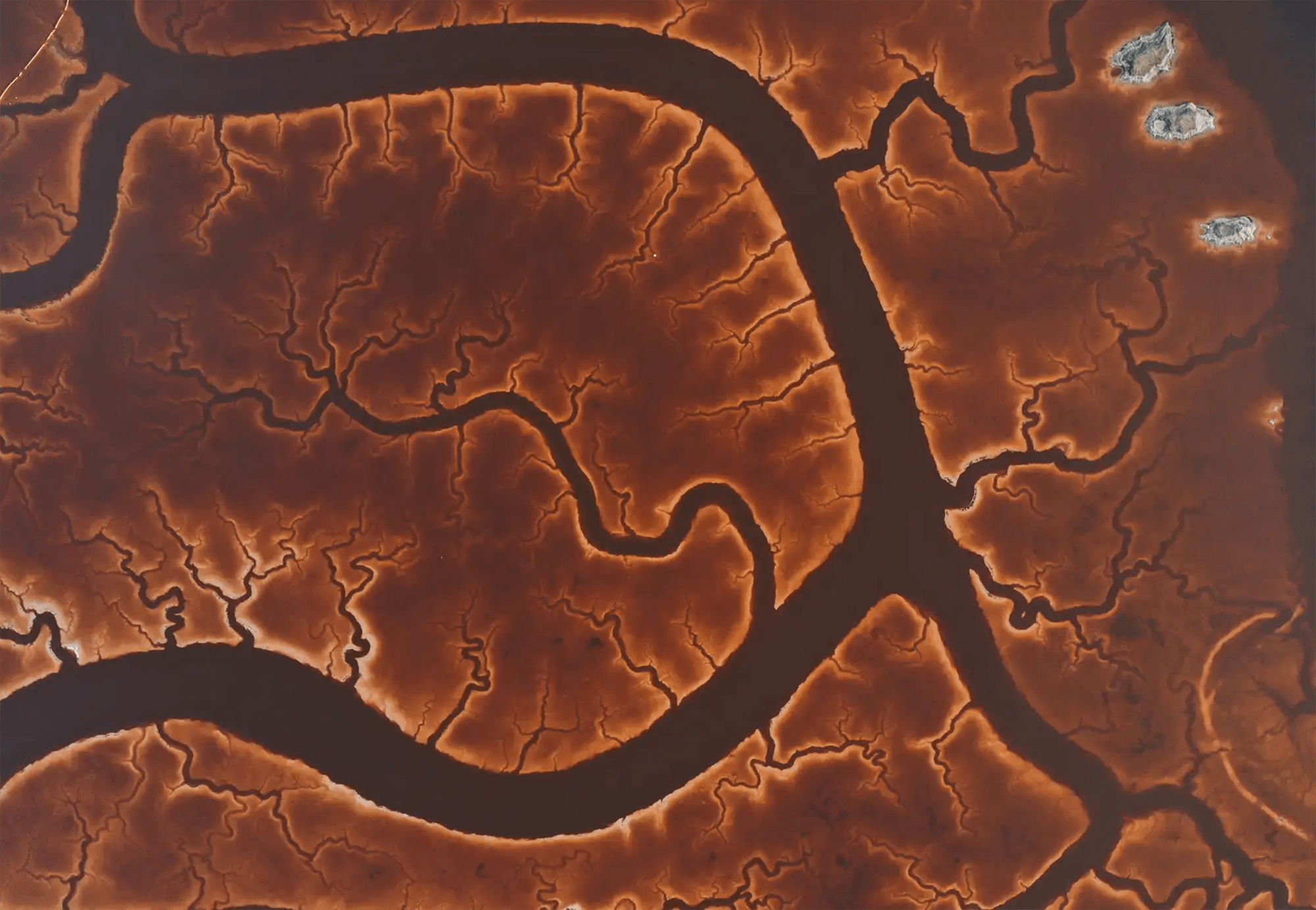
This award-winning aerial image by photographer Stuart Chape shows a tidal creek in Lake Cakora, New South Wales, Australia. At first glance, it looks much like any river delta, with branching dendritic paths that split into smaller and smaller waterways. That’s deceptive, though, because very different forces shape this creek. Because tides move in and out, a tidal creek is home to flows that move both directions — toward and away from the branches. That also means that flow speeds can change rapidly as the tides shift, which in turn changes which sediments get lifted, dropped, and moved around the creek bed. (Image credit: S. Chape/IAPOTY; via Colossal)
Tag: fractals

Fractal Fingers
As bizarre as the branching fractal fingers of the Saffman-Taylor instability look, they’re quite a common phenomenon. In his video, Steve Mould demonstrates how to make them by sandwiching a viscous liquid like school glue between two acrylic sheets and then pulling them apart. The more formal lab-version of this is the Hele-Shaw cell, which he also demonstrates. But you may have come across the effect when pealing up a screen protector or in dealing with a cracked phone screen. In all of these cases, a less viscous fluid — specifically air — is forcing its way into a more viscous fluid, something that it cannot manage without the fluid interface fracturing. (Video and image credit: S. Mould)

Why Nature Loves Fractals
Trees, blood vessels, and rivers all follow branching patterns that make their pieces look very similar to their whole. We call this repeating, self-similar shape a fractal, and this Be Smart video explores why these branching patterns are so common, both in living and non-living systems. For trees, packing a large, leafy surface area onto the smallest amount of wood makes sense; the tree needs plenty of solar energy (and water and carbon dioxide) to photosynthesize, and it has to be efficient about how much it grows to get that energy. Similarly, our lungs and blood vessels need to pack a lot of surface area into a small space to support the diffusion that lets us move oxygen and waste through our bodies. Non-living systems, like the branches of viscous fingers or river deltas or the branching of cracks and lightning, rely on different physics but wind up with the same patterns because they, too, have to balance forces that scale with surface area and ones that scale with volume. (Video and image credit: Be Smart)

Filling Space
While not directly fluid dynamical, this video from Steve Mould uses water to illustrate mathematical concepts like fractals and space-filling curves. Water, it turns out, does a great job of drawing our eyes to the way these one-dimensional curves fill up two- and three-dimensional space. Check out the full video for a mathematical dive into the concepts. (Video and image credit: S. Mould)

Marshy Veins
From above, the salt marshes of Alviso Marina County Park look like veins and capillaries in this photo from Tayfun Coskun. The waterways curve and branch, forming fractal patterns only apparent from the air. Although the mechanisms that form these dendritic patterns vary, they are very common in fluids, appearing over and over at many scales. (Image credit: T. Coskun; via Gizmodo)

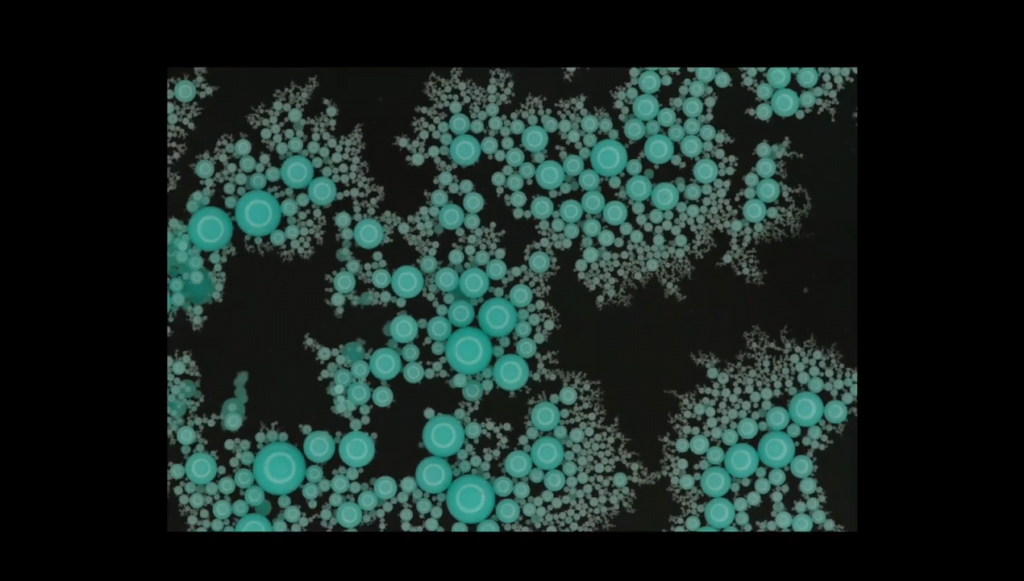
A Fractal Raft From a Spinning Top
File this one under Cool Things I Would Have Never Thought Of. In this video, researchers play around with the flow around a spinning top and end up creating a fractal, granular raft. By immersing a top in dyed fluid, they show the toroidal vortices that form around the spinning toy. Then, instead of dye, they add a stretchy elastomer compound that cures over time. The elastomer stretches into thin ligaments in the swirling flow around the top. Eventually, it breaks apart into spherical drops of all different sizes.
Once the top is removed, the elastomer drops slowly float to the surface. Surface tension and the Cheerios effect draw the drops together, and because of their many sizes, the rafts that form are fractal. (Image and video credit: B. Keshavarz and M. Geri)

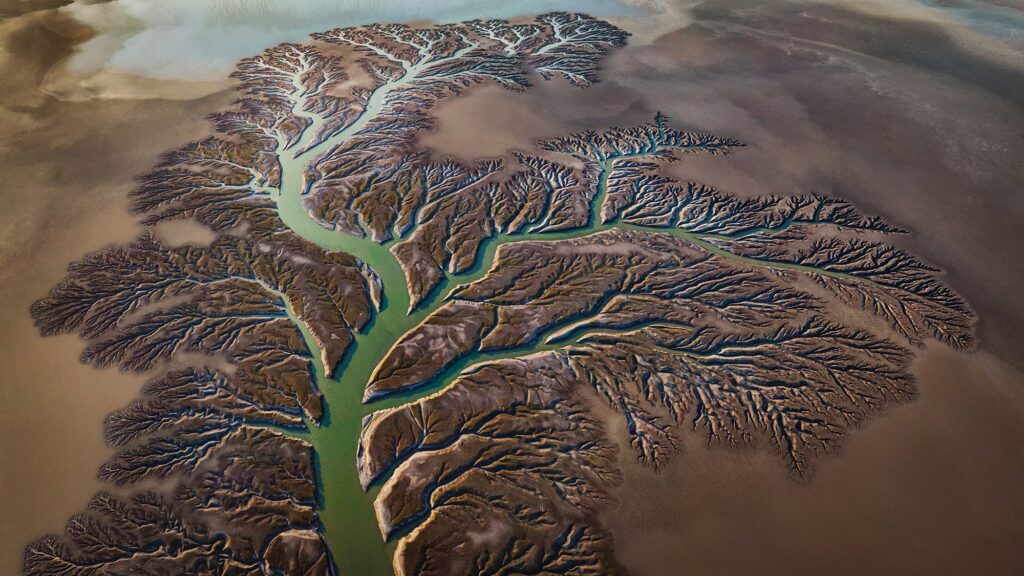
The Delta Series
It’s easy in the rush of our daily lives to forget just how dynamic rivers are. In his “Delta Series” conservation photographer Paul Nicklen explores that ever-changing nature from above the Colorado River delta. With the ongoing megadrought in this region and ever-increasing demands for more water, the Colorado no longer flows to the ocean. It trickles its way to a tired end near Baja, Mexico, where its last gasp is not enough to sustain ecosystems that relied on the river’s irrigation long before us. Nicklen’s work is a beautiful portrait of the fractal, tree-like patterns of a slowing river. Find more of Nicklen’s work on his website and Instagram. (Image credit: P. Nicklen; via Colossal)

The Kelvin-Helmholtz Instability
The Kelvin-Helmholtz instability is a pattern frequently found in nature. It has a distinctive shape, like a series of breaking ocean waves that curl over on themselves to create a string of vortices. The instability shows up when there is a velocity difference between two fluid layers. The unequal shear between the two layers magnifies any disturbance to their interface, which manifests in the fractal, overturning whorls seen in the numerical simulation above. You can find the Kelvin-Helmholtz instability in the lab, in the sky, in the ocean, on Jupiter and Mars–even on the sun! For more information on the methods used to create the simulation above, check out the full paper. (Video and research credit: K. Schaal et al.)

Reader Question: Fractals and Turbulence

Reader 3d-time asks:
Hi, there is a guy, at my college, who is doing a master’s degree thesis in turbulence. He says he uses fractals and computational methods. Can you explain how fractals can be used in fluid dynamics?
That’s a good question! Fractals are a relatively recent mathematical development, and they have several features that make them an attractive tool, especially in the field of turbulence. Firstly, fractals, especially the Mandelbrot set shown above, demonstrate that great complexity can be generated out of simple rules or equations. Secondly, fractals have a feature known as self-similarity, meaning that they appear essentially the same regardless of scale. If you zoom in on the Mandelbrot set, you keep finding copy after copy of the same pattern. Nature, of course, doesn’t have this perfect infinite self-similarity; at some point things break down into atoms if you keep zooming in. But it is possible to have self-similarity across a large range of scales. This is where turbulence comes in. Take a look at the turbulent plume of the volcanic eruption in the photo above. Physically, it contains scales ranging from hundreds of meters to millimeters, and these scales are connected to one another by their motion and the energy being passed from one scale to another. There have been theories suggested to describe the relationship between these scales, but no one has yet found a theory truly capable of explaining turbulence as we observe it. Both the self-similarity and the complex nature of fractals suggest they could be useful tools in finally unraveling turbulence. In fact, Mandelbrot himself wrote several papers connecting the two concepts. Perhaps your friend will help find the next hints! (Image credit: U.S. Geological Survey, Wikimedia)

Fluids Round-up – 16 November 2013
Time for another fluids round-up. Here are your links:
- PhysicsBuzz takes a look at the use of plasma actuators to control airflow.
- Over at Deep Sea News, you can learn about parasitic capillary waves.
- NanoWerk reports on self-steering particles in microfluidic devices.
- The 9th drop of the Queensland pitch drop experiment–believed to be the longest continuously running experiment in the world–is expected to fall at any time. Want to be part of the historic moment? Check out their Ninth Watch website.
- Aatish Bhatia examines the concepts behind the Fourier transform, an important mathematical technique used throughout fluid dynamics and physics. (via io9)
- Fluid dynamics and adaptive control might help alleviate traffic jams. (via @AIP_Publishing)
- On the whimsical side, take a look at these beautiful flying model boats built by Luigi Prina. (submitted by jshoer)
- Finally, our lead image was created with the app Frax, which allows users to make their own fractal-based art. Fluid dynamics has a lot of fractal behaviors. iOS users who want to play with fractals should check it out.
(Image credit: Ath3na)