Convective cells form as fluid is heated from below. As the fluid near the bottom warms, its density decreases and buoyancy causes it to rise while cooler fluid descends to replace it. This fluid motion due to temperature gradients is called Rayleigh-Benard convection and the cells in which the motion occurs are called Benard cells. This particular type of convection is essentially what happens when a pot is placed on a hot stove, so the shapes are familiar. Similar shapes also form on the sun’s photosphere, where they are called granules.
Tag: convection

Science Off the Sphere: Liquid Lenses
Astronaut Don Pettit delivers more “Science Off The Sphere” in his latest video. Here he demonstrates diffusion and convection in a two-dimensional water film in microgravity. He notes that the viscous damping in the water is relatively low and that, left undisturbed, mixing in the film will continue for 5-10 minutes before coming to rest, which tells us that the Reynolds numbers of the flow are reasonably large. The structures formed are also intriguing; he notes that drops mix with mushroom-like shapes that are reminiscent of Rayleigh-Taylor instabilities and cross-sectional views of vortex rings. It would be interesting to compare experiments from the International Space Station with earthbound simulations of two-dimensional mixing and turbulence, given that the latter behaves so differently in 2D.

Science off the Sphere: Thin Films
Stuck here on Earth, it’s hard to know sometimes how greatly gravity affects the behavior of fluids. Fortunately, astronaut Don Pettit enjoys spending his free time on the International Space Station playing with physics. In his latest video, he shows some awesome examples of what is possible with a thin film of water–not a soap film like we make here on Earth–in microgravity. He demonstrates vibrational modes, droplet collision and coalescence, and some fascinating examples of Marangoni convection.

Convection Visualization
Here on Earth a fascinating form of convection occurs every time we put a pot of water on the stove. As the fluid near the burner warms up, its density decreases compared to the cooler fluid above it. This triggers an instability, causing the cold fluid to drift downward due to gravity while the warm fluid rises. Once the positions are reversed, the formerly cold fluid is being heated by the burner while the formerly hot fluid loses its heat to the air. The process continues, causing the formation of convection cells. The shapes these cells take depend on the fluid and its boundary conditions. For the pot of water on the stove and in the video above, the surface tension of the air/water interface can also play a role in modifying the shapes formed. The effects caused by the temperature gradient are called Rayleigh-Benard convection. The surface tension effects are sometimes called Benard-Marangoni convection.

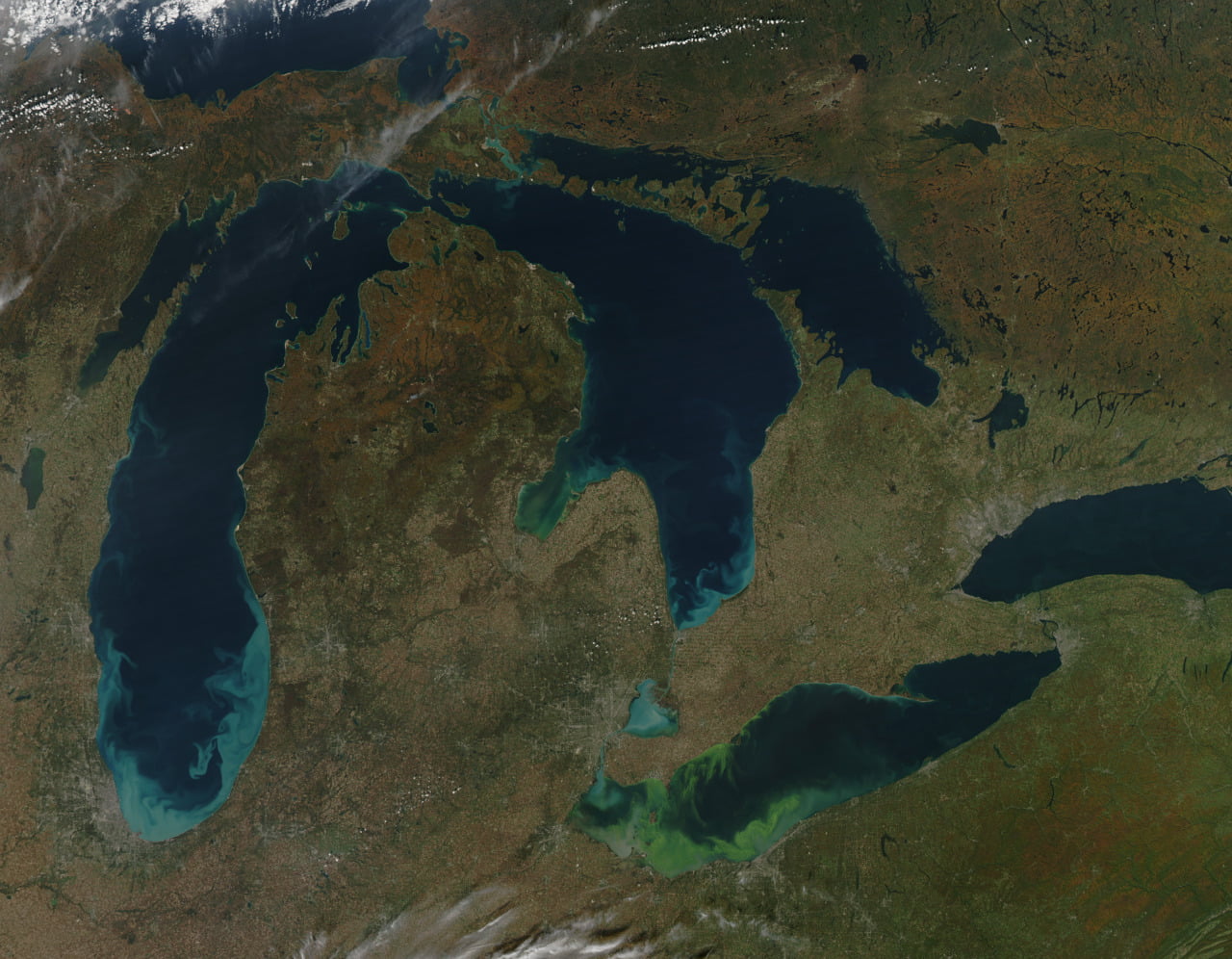
Stirred Up Sediment
Swirls of blue in the Great Lakes mark locations of recent autumn storms whose winds have stirred up sediment in the lakes. The silt and quartz sand acts as a tracer particle, making visible the circulation patterns of the lakes. In contrast, the green streaks mark locations of calmer winds and warmer temperatures where algae blooms have grown. Note the fundamental dissimilarity in their structures. Blue eddies turn over and mix in a fashion reminiscent of convective instabilities while the green blooms are far more uniform in structure. #

2D Convection
This simulation shows 2D Rayleigh-Benard convection in which a fluid of uniform initial temperature is heated from below and cooled from above. This is roughly analogous to the situation of placing a pot of water on a hot stovetop. (In the case of the water on the stove, the upper boundary is the water-air interface, while, in the simulation, the upper boundary is modeled as a no-slip (i.e. solid) interface.) The simulation shows contours of temperature (black = cool, white = hot). In general, the hot fluid rises and the cold fluid sinks due to differences in density, but, as the simulation shows, the actual mixing that occurs is far more complex than that simple axiom indicates.

Cloud Streets
Cloud streets–long rows of counter-rotating air parallel to the ground in the planetary boundary layer–are thought to form as a result of cold air blowing over warm waters while caught beneath a warmer layer of air, a temperature inversion. As moisture evaporates from the warmer water, it creates thermal updrafts that rise through the atmosphere until they hit the temperature inversion. With nowhere to go, the warmer air tends to lose its heat to the surroundings and sink back down, creating a roll-like convective cell. (Photo credits: NASA Terra, NASA Aqua, and Tatiana Gerus)

Un-Mixing a Fluid Demo
Not only is this demonstration one of my favorites, it’s a reader favorite, too. Even though I posted it nearly a year ago, I’ve had it resubmitted over and over. Here’s what I originally wrote:
Laminar flow (as opposed to turbulence) has the interesting property of reversibility. In this video, physicists demonstrate how flow between concentric cylinders can be reversed such that the initial fluid state is obtained (to within the limits of molecular diffusion, of course!)
For more examples, see the first half of this video.
The results of those videos might be surprising, but they highlight the difference between laminar flow and turbulence. In laminar flow, the motion of the dye is caused by molecular diffusion and momentum diffusion, the latter of which is exactly reversible. In turbulence, much of the fluid motion is tied up in momentum convection, which is irreversible. This is why you can “unstir” the glycerin but not the milk in your coffee.

Aurora Physics
The auroras at Earth’s poles are much more than pretty lights. This video explains their formation; fluid mechanics (specifically magnetohydrodynamics) play a major role in the convective transport of heat inside the sun as well as the movement of the plasma that makes up a solar storm that interacts with Earth’s magnetic field and produces the auroras.

Solutal Convection
Solutal convection, rather than relying on temperature gradients, can occur due to gradients in concentration or in surface tension. While less spectacular than this previously posted video, this video contains a nice simplified explanation of the mechanism. And, as noted in the video, this is a demo you can do yourself at home.