Tag: transitional flow

Dripping Down the Rivulet
If you’ve ever watched water running down the side of the street, you’ve probably noticed that it doesn’t flow smoothly. Instead, you’ll see waves, rivulets, and disturbances that form. That’s because the simple action of flowing down an incline is unstable. Water and other viscous liquids can’t flow downhill smoothly. Any disturbances – an uneven surface, the rumble of passing cars, a pebble in the way – will create a disruption that grows, often until the entire flow is affected. This video shows some of the complex and beautiful patterns you get then. (Video and image credit: G. Lerisson et al.)
January 18, 2019
Spillway Waves
Earlier this summer, the spillway of the Banja Dam was opened for the first time, releasing a stream of excess water from the reservoir. As you can see above, waves quickly formed at the surface of the falling water. You’ve likely noticed this yourself in the run-off along the street after a storm. It turns out that shallow water running down an incline is unstable. A disturbance to the flow – from surface roughness, vibration, or a change in curvature – will grow, just like a ball sitting at the top of a hill will roll down as soon as it’s prodded. For more about this kind of instability, check out this post or my video about boundary layer stability and the Space Shuttle. (Image credit: Guillaume TYTECA, source; via Gizmodo)
August 3, 2016
Frisbee Physics, Part 2
Yesterday we discussed some of the basic mechanics of a frisbee in flight. Although frisbees do generate lift similarly to a wing, they do have some unique features. You’ve probably noticed, for example, that the top surface of a frisbee has several raised concentric rings. These are not simply decoration! Instead the rings disrupt airflow at the surface of the frisbee. This actually creates a narrow region of separated flow, visible in region B on the left oil-flow image. Airflow reattaches to the frisbee in the image after the second black arc, and the boundary layer along region C remains turbulent and attached for the remaining length of the frisbee. Keeping the boundary layer attached over the top surface ensures low pressure so that the disk has plenty of lift and remains aerodynamically stable in flight. A smooth frisbee would be much harder to throw accurately because its flight would be very sensitive to angle of attack and likely to stall. (Image credits: J. Potts and W. Crowther; recommended papers by: V. Morrison and R. Lorentz)
August 26, 2014
Incense in Transition
A buoyant plume of smoke rises from a stick of incense. At first the plume is smooth and laminar, but even in quiescent air, tiny perturbations can sneak into the flow, causing the periodic vortical whorls seen near the top of the photo. Were the frame even taller, we would see this transitional flow become completely chaotic and turbulent. Despite having known the governing equations for such flow for over 150 years, it remains almost impossible to predict the point where flow will transition for any practical problem, largely because the equations are so sensitive to initial conditions. In fact, some of the fundamental mathematical properties of those equations remain unproven. (Photo credit: M. Rosic)
May 31, 2013
Swirling Jets
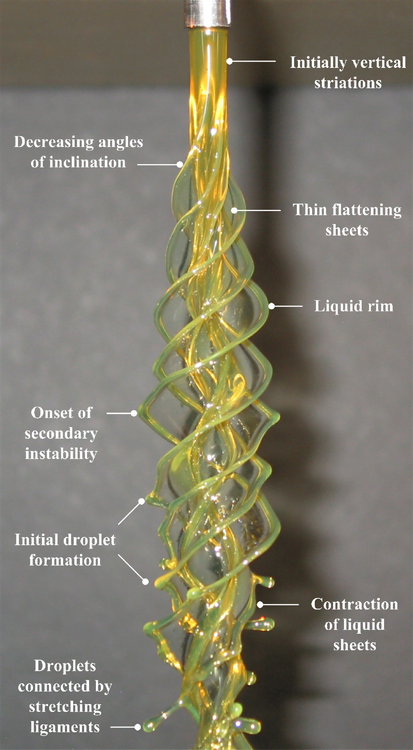
In fluid dynamics, we like to classify flows as laminar–smooth and orderly–or turbulent–chaotic and seemingly random–but rarely is any given flow one or the other. Many flows start out laminar and then transition to turbulence. Often this is due to the introduction of a tiny perturbation which grows due to the flow’s instability and ultimately provokes transition. An instability can typically take more than one form in a given flow, based on the characteristic lengths, velocities, etc. of the flow, and we classify these as instability modes. In the case of the vertical rotating viscous liquid jet shown above, the rotation rate separates one mode (n) from another. As the mode and rotation rate increase, the shape assumed by the rotating liquid becomes more complicated. Within each of these columns, though, we can also observe the transition process. Key features are labeled in the still photograph of the n=4 mode shown below. Initially, the column is smooth and uniform, then small vertical striations appear, developing into sheets that wrap around the jet. But this shape is also unstable and a secondary instability forms on the liquid rim, which causes the formation of droplets that stretch outward on ligaments. Ultimately, these droplets will overcome the surface tension holding them to the jet and the flow will atomize. (Video and photo credits: J. P. Kubitschek and P. D. Weidman)
December 6, 2012
Transition to Turbulence
Smoke introduced into the boundary layer of a cone rotating in a stream highlights the transition from laminar to turbulent flow. On the left side of the picture, the boundary layer is uniform and steady, i.e. laminar, until environmental disturbances cause the formation of spiral vortices. These vortices remain stable until further growing disturbances cause them to develop a lacy structure, which soon breaks down into fully turbulent flow. Understanding the underlying physics of these disturbances and their growth is part of the field of stability and transition in fluid mechanics. (Photo credit: R. Kobayashi, Y. Kohama, and M. Kurosawa; taken from Van Dyke’s An Album of Fluid Motion)
November 15, 2011
Smoke Transition
Smoke issuing from a round jet undergoes transition from laminar to turbulent flow. As the smoke moves past the unmoving ambient air, the friction between these two layers creates shear and triggers a Kelvin-Helmholtz instability, recognizable by the formation and roll up of vortices along the edges of the jet. Those vortices then roll together in pairs, detach, and devolve into a generally turbulent flow. Because turbulence is far more efficient at mixing than a laminar flow is, the smoke seems to disappear.
October 17, 2011
Toroidal Vortex
When instabilities exist in laminar flow, they do not always lead immediately to turbulence. In this video, a viscous fluid fills the space between two concentric cylinders. As the inner cylinder rotates, a linear velocity profile (as viewed from above) forms; this is known as Taylor-Couette flow. If any tiny perturbations are added to that linear profile–say there is a nick in the surface of one of the cylinders–the flow will develop an instability. In this type of flow, an exchange of stabilities will occur. Rather than transitioning to turbulence, the fluid develops a stable secondary flow–the toroidal vortex highlighted by the dye in the video. If the rotation rate is increased further other instabilities will develop.
August 31, 2011
Reynolds on Transition
For although only the disciplined motion is recognized in military tactics, troops have another manner of motion when anything disturbs their order. And this is precisely how it is with water: it will move in a perfectly direct disciplined manner under some circumstances, while under others it becomes a mass of eddies and cross streams, which may be well likened to the motion of a whirling, struggling mob where each individual particle is obstructing the others. The larger the army, and the more rapid the evolutions, the greater the chance of disorder; so with ﬂuid, the larger the channel, and the greater the velocity, the more chance of eddies.
Osborne Reynolds, on the transition from laminar to turbulent flow
March 30, 2011
Godspeed, Discovery!
The space shuttle, despite three decades of service, remains a triumph of engineering. Although it is nominally a space vehicle, fluid dynamics are vital throughout its operation. From the combustion in the engine to the overexpansion of the exhaust gases; from the turbulent plume of the shuttle’s wake to the life support and waste management systems on orbit, fluid mechanics cannot be escaped. Countless simulations and experiments have helped determine the forces, temperatures, and flight profiles for the vehicle during ascent and re-entry. Experiments have flown as payloads and hundreds of astronauts have “performed experiments in fluid mechanics” in microgravity. Since STS-114, flow transition experiments have even been mounted on the orbiter wing. The effort and love put into making these machines fly is staggering, but all things end. Godspeed to Discovery and her crew on this, her final mission!
February 25, 2011