A buoyant plume of smoke rises from a stick of incense. At first the plume is smooth and laminar, but even in quiescent air, tiny perturbations can sneak into the flow, causing the periodic vortical whorls seen near the top of the photo. Were the frame even taller, we would see this transitional flow become completely chaotic and turbulent. Despite having known the governing equations for such flow for over 150 years, it remains almost impossible to predict the point where flow will transition for any practical problem, largely because the equations are so sensitive to initial conditions. In fact, some of the fundamental mathematical properties of those equations remain unproven. (Photo credit: M. Rosic)
Search results for: “transition”

Transition to Turbulence
Smoke introduced into the boundary layer of a cone rotating in a stream highlights the transition from laminar to turbulent flow. On the left side of the picture, the boundary layer is uniform and steady, i.e. laminar, until environmental disturbances cause the formation of spiral vortices. These vortices remain stable until further growing disturbances cause them to develop a lacy structure, which soon breaks down into fully turbulent flow. Understanding the underlying physics of these disturbances and their growth is part of the field of stability and transition in fluid mechanics. (Photo credit: R. Kobayashi, Y. Kohama, and M. Kurosawa; taken from Van Dyke’s An Album of Fluid Motion)

Smoke Transition
Smoke issuing from a round jet undergoes transition from laminar to turbulent flow. As the smoke moves past the unmoving ambient air, the friction between these two layers creates shear and triggers a Kelvin-Helmholtz instability, recognizable by the formation and roll up of vortices along the edges of the jet. Those vortices then roll together in pairs, detach, and devolve into a generally turbulent flow. Because turbulence is far more efficient at mixing than a laminar flow is, the smoke seems to disappear.

Osborne Reynolds and Transition

How and when flow through a pipe becomes turbulent has been a conundrum for fluid mechanicians since the days of Osbourne Reynolds (~1870s):
Typically, the laminar-to-turbulence transition is studied mathematically by linearizing the Navier-Stokes equations, the governing equations of fluid dynamics, then perturbing the system. These perturbations will gradually disappear in laminar flow, but if the flow is turbulent, they’ll grow and produce chaotic motion. The transition, then, is the critical point between these two.
However, for pipe flows, this linearized approach shows that the perturbations decay for all Reynolds numbers, even though this doesn’t happen in actual experiments. In the real world, as the Reynolds number increases, small, turbulent puffs begin to split and interact, and their lifetimes increase. Eventually, these puffs carry enough turbulence to transition the flow entirely. # (submitted by David T)
Reynolds on Transition
For although only the disciplined motion is recognized in military tactics, troops have another manner of motion when anything disturbs their order. And this is precisely how it is with water: it will move in a perfectly direct disciplined manner under some circumstances, while under others it becomes a mass of eddies and cross streams, which may be well likened to the motion of a whirling, struggling mob where each individual particle is obstructing the others. The larger the army, and the more rapid the evolutions, the greater the chance of disorder; so with fluid, the larger the channel, and the greater the velocity, the more chance of eddies.

A New Plasma Wave for Jupiter
Jupiter‘s North Pole has a powerful magnetic field combined with plasma that has unusually low electron densities. This combination, researchers found, gives rise to a new type of plasma wave.
Ions in a magnetic field typically move parallel to magnetic field lines in Langmuir waves and perpendicularly to the field lines in Alfvén waves — with each wave carrying a distinctive frequency signature. But in Jupiter’s strong magnetosphere, low-density plasma does something quite different: it creates what the team is calling an Alfvén-Langmuir wave — a wave that transitions from Alfvén-like to Langmuir-like, depending on wave number and excitation from local beams of electrons.
Although this is the first time such plasma behavior has been observed, the team suggests that other strongly-magnetized giant planets — or even stars — could also form these waves near their poles. (Image credit: NASA / JPL-Caltech / SwR I/ MSSS/G. Eason; research credit: R. Lysak et al.; via APS)

Bow Shock Instability
There are few flows more violent than planetary re-entry. Crossing a shock wave is always violent; it forces a sudden jump in density, temperature, and pressure. But at re-entry speeds this shock wave is so strong the density can jump by a factor of 13 or more, and the temperature increase is high enough that it literally rips air molecules apart into plasma.
Here, researchers show a numerical simulation of flow around a space capsule moving at Mach 28. The transition through the capsule’s bow shock is so violent that within a few milliseconds, all of the flow behind the shock wave is turbulent. Because turbulence is so good at mixing, this carries hot plasma closer to the capsule’s surface, causing the high temperatures visible in reds and yellows in the image. Also shown — in shades of gray — is the vorticity magnitude of flow around the capsule. (Image credit: A. Álvarez and A. Lozano-Duran)

Predicting Yield
We’ve all experienced the frustration of ketchup refusing to leave the bottle or toothpaste that shoots out suddenly. These materials are yield stress fluids, which transition from solid-like behavior to liquid flow once the right amount of force is applied. A new study suggests that — despite their wide range of characteristics — these fluids share a universal relation: their yield transition (when they start to flow) depends on their characteristics when at rest. Interestingly, this relationship seems to hold not only for polymeric fluids like the one in the study but also nonpolymeric ones. (Image credit: haideyy; research credit: D. Keane et al.; via APS Physics)

Dams Fill Reservoirs With Sediment
Dams are critical pieces of infrastructure, but, as Grady shows in this Practical Engineering video, they are destined to be temporary. The reason is that they naturally fill with sediment over time. Rivers carry a combination of water and sediment; the latter is critical to healthy shorelines and stable ecology. But while sediment gets carried along by a fast-flowing river, slower flow rates allow sediment to fall out of suspension, as demonstrated in Grady’s tabletop flume. As his river transitions to a deeper, slower-flowing reservoir, sand falls out of the flow, building up colorful strata. The sand and water even create dynamic feedback loops, as seen with the dunes that form in his timelapse and march toward the dam.
Any long-term plan for a dam has to deal with this inevitable build-up of sediment, and, unfortunately, it’s not a simple or cheap problem to address, as discussed in the video. (Video and image credit: Practical Engineering)
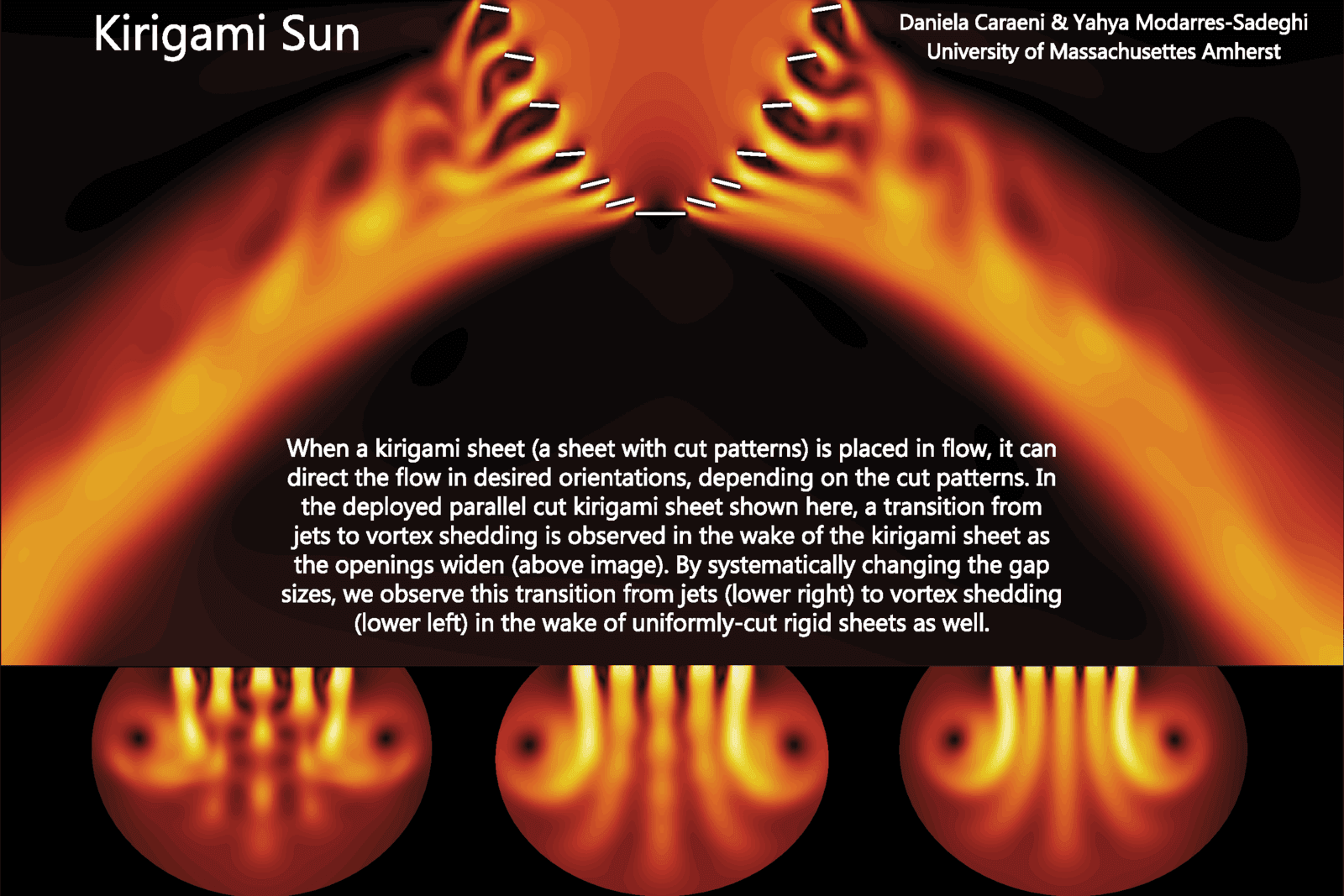
“Kirigami Sun”
Kirigami is a variation of origami in which paper can be cut as well as folded. Here, researchers look at flow through a cut kirigami sheet and how that flow changes with the cuts’ length. In the top central image, white lines mark the paper boundaries. As the cut gaps get larger, flow through them transitions from a continuous jet to swirling vortex shedding. Along the bottom, we see similar patterns emerge in the wake of uniformly-cut sheets, too. On the right, the flow comes through in jets; moving leftward, it transitions to an unsteady vortex shedding flow. (Image credit: D. Caraeni and Y. Modarres-Sadeghi)



