Computational fluid dynamics (CFD) sometimes gets a bad rep as “colorful fluid dynamics”, but as computers get faster and faster, more complicated and physically accurate simulations are possible. Shown here are simulations of vortex rings and wingtip vortices in stunningly gorgeous detail. Understanding the evolution of these vortices from a fundamental level helps fluid mechanicians design better methods of controlling them. As mentioned in the video, wingtip vortices are a particularly hazardous everyday example; the time it takes for one plane’s wingtip vortices to disperse determines how quickly the next airplane can take-off or land on that same runway. Being able to break down these vortices faster would allow more frequent use of existing facilities.
Tag: computational fluid dynamics

Swimming Sandfish Lizards
Sandfish lizards can “swim” through granular flows like sand using an undulating, sinusoidal motion. Having studied this motion, engineers have built a robot that swims similarly through large glass beads and have now created a numerical simulation of the physics that matches the measured forces on the swimmer to within 8%. This type of flow is, in some respects, tougher than actual fluids because individual particles have to followed, while in most of fluid mechanics, we can use the continuum assumption to treat a liquid or gas as a continuous medium. #

Volcanic Turbulence
One of the characteristics of turbulence is its large range of lengthscales. Consider the ash plume from this Japanese volcano. Some of the eddy structures are tens, if not hundreds, of meters in size, yet there is also coherence down to the scale of centimeters. In turbulence, energy cascades from these very large scales to scales small enough that viscosity can dissipate it. This is one of the great challenges in directly calculating or even simply modeling turbulence because no lengthscale can be ignore without affecting the accuracy of the results. #

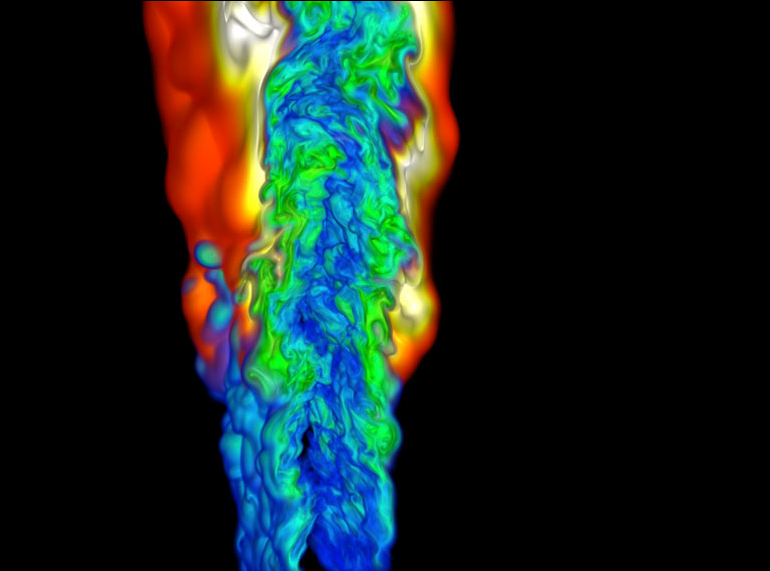
Colorful Computational Combustion
Many fluid dynamics problems are so complicated that they require supercomputers to calculate the mathematical and physical details. This image shows a computer simulation of a cold ethylene jet combusting in hot air. Different colors indicate different combustion by-products. Researchers use simulations like this one to investigate ideal flames that improve efficiency in applications like cars or jet engines. #

Starting a Rocket
This computational fluid dynamics (CFD) simulation shows the start-up of a two-dimensional, ideal rocket nozzle. Starting a rocket engine or supersonic wind tunnel is more complicated than its subsonic counterpart because it’s necessary for a shockwave to pass completely through the engine (or tunnel), leaving supersonic flow in its wake. Here the situation is further complicated by turbulent boundary layers along the nozzle walls. (Video credit: B. Olson)

Kelvin-Helmholtz Instability
The Kelvin-Helmholtz instability occurs when velocity shear is present in a single fluid or when two different fluids have a velocity difference across their interface. As shown in this numerical simulation, the instability produces a fractal-like pattern of eddies turning over on themselves. The Kelvin-Helmholtz instability is commonly found in nature between cloud layers. #
ETA: It looks like animated GIFs may not work with Tumblr. Be sure to click on the picture to see the animation on Wikipedia.

Flow Visualization
This video, created by undergraduates as part of a fluid dynamics laboratory course, shows flow visualization of a von Karman vortex street in the wake of a cylinder in comparison to a computational fluid dynamics (CFD) simulation of the same phenomenon. If you’re wondering about the black-and-white segments and the peculiar speech patterns, look no further. The students are parodying a series of videos made by MIT in the 1960s that are still used in classrooms today.