FYFD

Tag: stability

  • Flipping Icebergs

    Flipping Icebergs

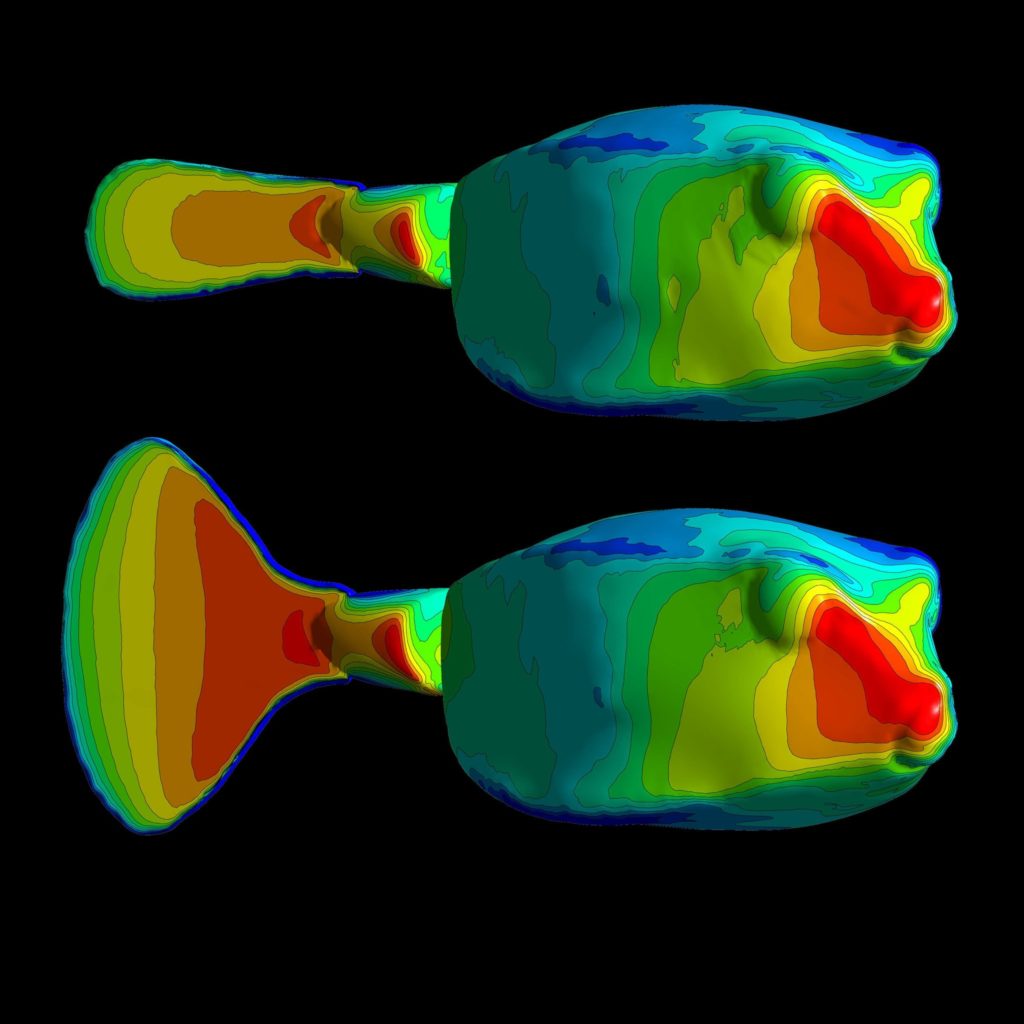
    When an iceberg flips, it creates waves that can endanger ships nearby, but the move can also trigger further melting. In the ocean, many factors, including wind and waves, can contribute to an iceberg flipping, so researchers studied small, lab-scale versions to see how melting–alone–affects an iceberg’s likelihood of flipping.

    The results showed that melting alone was enough to destabilize icebergs and make them flip, as seen in the timelapse above. These mini-icebergs melted faster underwater, changing the berg’s overall shape and eventually triggering a flip. Corners developed at the waterline where the different melt rates above- and below-the-water met. Whenever a flip occurred, one of these corners would always settle at the new water line, causing the lab iceberg to change from a circular cylinder to a polygon as melting continued. (Image credit: M. Whiston; research and video credit: B. Johnson et al.; via APS)

    Fediverse Reactions
  • Stabilizing Paper Airplanes

    Stabilizing Paper Airplanes

    Making a good paper airplane is tough. Drop a simple sheet of paper and it will tumble and flip its way to the floor instead of gliding. The folds of a proper paper airplane add weight in just the right spots to stabilize its flight and let it glide smoothly through the air. To better understand what makes paper fly, researchers looked at how sheets of paper flew when weighted (with metallic tape) in different spots.

    Trajectories of pieces of paper with different weighting.
    Trajectories of pieces of paper with different weighting.

    An unweighted sheet of paper tumbled end-over-end. Shifting the center-of-mass too far forward or backwards also resulted in tumbles and nosedives. But when the weighting placed the center of mass between these two extremes, there was a sweet spot where the paper glided smoothly. In this situation, the aerodynamic forces on the paper could correct for changes in flight angle; if the paper tilted too far upward, the forces pushed it back down — and vice versa. This ability of the thin wing to self-stabilize is different than most large-scale aircraft, which need tails and other structures to provide stability to the main wing. (Image credit: paper airplane – K. Eliason, paper trajectories – H. Li et al.; research credit: H. Li et al.; via Ars Technica; submitted by Kam-Yung Soh)

  • Stabilizing Foams

    Stabilizing Foams

    Bubbles in a pure liquid don’t last long, but with added surfactants or multiple miscible liquids, bubbles can form long-lasting foams. In soapy foams, surfactants provide the surface tension gradients necessary to keep the thin liquid layers between bubbles from popping. But what stabilizes a surfactant-free foam?

    New work finds that foams in mixtures of two miscible fluids only form when the surface tension depends nonlinearly on the concentration of the component liquids. When this is true, thinning the wall between bubbles creates changes in surface tension that stabilize the barrier and keep it from popping.

    In mixtures without this nonlinearity, foams just won’t form. The new results are valuable for manufacturing, where companies can avoid unintentional foams simply by careful selection of their fluids. (Image credit: G. Trovato; research credit: H. Tran et al.; via APS Physics; see also Ars Technica, submitted by Kam-Yung Soh)

  • Adjusting for Gusts

    Adjusting for Gusts

    In flight, birds must adjust quickly to wind gusts or risk crashing. Research shows that the structure of birds’ wings enables them to respond faster than their brains can. The wings essentially act like a suspension system, with the shoulder joint allowing them to lift rapidly in response to vertical gusts. This motion keeps the bird’s head and torso steady, so they can focus on more complex tasks like landing, obstacle avoidance, and prey capture. (Image and research credit: J. Cheney et al.; submitted by Kam-Yung Soh)

  • Floating in Levitating Liquids

    Floating in Levitating Liquids

    When it comes to stability, nature can be amazingly counter-intuitive, as in this case of flotation on the underside of a levitating liquid. First things first: how is this liquid layer levitating? To answer that, consider a simpler system: a pendulum. There are two equilibrium positions for a pendulum: hanging straight down or pointing straight up. We don’t typically observe the latter position because it’s unstable; the slightest disturbance from that perfectly vertical situation will make it fall. But it’s possible to stabilize an inverted pendulum simply by shaking it up and down. The vibration creates a dynamic stability.

    The same physics, it turns out, holds for a layer of viscous fluid. With the right vibration, the denser fluid can levitate stably over a layer of air. Inside this vibrating layer, the rules of buoyancy are a little different because the vibration modifies the effects of gravity. As a result, bubbles deep in the liquid layer sink (Image 1). The researchers used this behavior to create their levitating layer (Image 2). The shaking also serves to stabilize objects floating on the underside of the liquid layer, allowing the boat in Image 3 to float upside down! (Image and research credit: B. Apffel et al.; via NYTimes; submitted by multiple sources)

  • Featured Video Play Icon

    The Magic* Cork

    *Spoiler alert: it’s not magic. It’s science!

    Just what makes this dropped cork float beneath the surface? Just like a normal cork, it’s buoyancy! But this seemingly straightforward video is hiding a few key elements. Firstly, the cork has been modified; it has a metal sphere inside it so that its effective density is higher than that of water.

    Secondly, that liquid is not pure water; notice the hazy swirls near the bottom of the flask when the cork drops in? This is tap water that’s had a layer of salt dissolving in the bottom of it for the last day. That creates a density gradient with denser, salty water at the bottom and lighter, fresh water at the top. In fluid dynamics, we’d say the fluid is stably stratified; “stratified” meaning that there are distinct layers (strata) of different density and “stably” because the heavier ones are at the bottom.

    When the cork is dropped in, it settles at the fluid layer that matches its density. Because the surrounding fluid is stably stratified, poking the cork makes it bounce slightly but return to its initial height. Our atmosphere behaves just like this when it’s stably stratified. If you displace a parcel of air, it will oscillate up and down before settling back to equilibrium. In fact, the cork and the air even bounce at the same frequency! (Video and submission credit: F. Croccolo)

  • Undulating Keeps Flying Snakes Steady

    Undulating Keeps Flying Snakes Steady

    Flying snakes undulate through the air as they glide. But, unlike on land, these wiggles aren’t for propulsion. A new study shows instead that they are key to the snake staying stable in flight.

    Upon take-off, a flying snake flattens its body, forming a wing-like shape that helps them generate lift and control drag. But while they glide, they also slither and pitch their tail.

    Researchers recorded more than 150 flights by live snakes, then used that data to construct their own digital snake. The model could fly like a real snake or be tested without undulations to see what would happen. The researchers discovered that, without that mid-air slithering, the snake quickly lost control and rolled to the side. (Image and research credit: I. Yeaton et al.; via NYTimes; submitted by Kam-Yung Soh)

  • Steering as a Boxfish

    Steering as a Boxfish

    Coral reefs are full of odd-looking denizens, but one of the funniest-looking ones must be the boxfish. This family of fish lives up to its name; their bodies feature an angular, bony carapace that helps protect them. But you don’t have to be a fluid dynamicist to wonder how in the world they swim with that kind of shape.

    There’s actually disagreement in scientific circles as to whether the basic shape of a boxfish is stabilizing or destabilizing, in other words, whether the fish’s body shape will try to automatically turn or roll when flow moves past. A new study focuses instead on the role the fish’s tail fin serves. Through experiments (on a fish model) and simulations, the researchers showed that boxfish rely on their tail fins both as rudders and course-stabilizers.

    Living around coral reefs means that boxfish need to be highly maneuverable, and this research indicates that the fish’s body shape, combined with the stabilizing power of its tail, are key to its ability to quickly and easily turn in any direction. (Image credits: boxfish – D. Seddon, simulation – P. Boute et al.; research credit: P. Boute et al.; via NYTimes; submitted by Kam-Yung Soh)

  • Keeping Bubbles Around

    Keeping Bubbles Around

    Bubbles don’t stick around in pure water. Surfactants are needed to stabilize the thin liquid film for longer than the blink of an eye. But that’s not necessarily the case for other liquids. As the video below shows, a bubble in isopropyl alcohol is quite stable. This is because of the alcohol’s volatility – its ability to evaporate easily.

    As the alcohol in the bubble film evaporates, it cools the film, creating a difference in surface tension that pulls fresh alcohol up into the bubble film. It’s so efficient at pulling alcohol up that the alcohol can’t evaporate fast enough to use it all. Once the excess alcohol is heavy enough, it slides back down the side of the bubble. Overall, though, the process is enough to keep a bubble in pure isopropyl alcohol from rupturing for minutes to hours at a time. (Image and video credit: M. Menesses et al.)

  • What Makes Turbulence So Hard

    What Makes Turbulence So Hard

    Turbulence – that pestersome, unpredictable, and chaotic state of flow – has been a thorn in the sides of mathematicians, physicists, and engineers for centuries. It is certainly one of – if not the – oldest unsolved problem in physics. Over at Ars Technica, Lee Phillips has a nice overview of the situation, including what makes the problem so difficult:

    The Navier-Stokes equation is difficult to solve because it is nonlinear. This word is thrown around quite a bit, but here it means something specific. You can build up a complicated solution to a linear equation by adding up many simple solutions. An example you may be aware of is sound: the equation for sound waves is linear, so you can build up a complex sound by adding together many simple sounds of different frequencies (“harmonics”). Elementary quantum mechanics is also linear; the Schrödinger equation allows you to add together solutions to find a new solution.

    But fluid dynamics doesn’t work this way: the nonlinearity of the Navier-Stokes equation means that you can’t build solutions by adding together simpler solutions. This is part of the reason that Heisenberg’s mathematical genius, which served him so well in helping to invent quantum mechanics, was put to such a severe test when it came to turbulence. 

    Phillips goes on to describe some of the many methods researchers use to unravel the mysteries of turbulence computationally, experimentally, and theoretically. This is a great introduction for those curious to get a sense of how turbulence, stability theory, and computational fluid dynamics all fit together. (Image credits: L. Da Vinci; NASA; see also: Ars Technica; submitted by Kam Yung-Soh)