Turbulent flows are ubiquitous, but they’re also mindbogglingly complex: ever-changing in both time and space across length scales both large and small. To try to unravel this complexity, scientists use simplified model problems. One such simplification is Kolmogorov flow: an imaginary flow where the fluid is forced back and forth sinusoidally. This large-scale forcing puts energy into the flow that cascades down to smaller length scales through the turbulent energy cascade. Here, researchers depict a numerical simulation of a turbulent Kolmogorov flow. The colors represent the flow’s vorticity field. Notice how your eye can pick out both tiny eddies and larger clusters in the flow; those patterns reflect the multi-scale nature of turbulence. (Image credit: C. Amores and M. Graham)
Tag: turbulent energy cascade

Testing Turbulence’s Limits
Understanding chaotic, turbulent flows has long challenged scientists and engineers due to their sheer complexity. In turbulent flows, energy cascades from the largest scales — like the kilometer-size cross-section of a cloud — to the very smallest scales, less than a millimeter in size, where viscosity transforms the flow’s motion to heat. For nearly a century, our theoretical understanding of turbulence has posited that there are certain universal behaviors in the statistics of a turbulent flow — essentially that, due to this energy cascade, some aspects of every turbulent flow are the same from clouds to ocean currents to your coffee cup.
Accordingly, experimentalists have tried for decades to measure this expected universality. Often, there are some signs of agreement, and any deviation was attributed to the finite difference between the large and small scales of the flow. (The theory assumes the difference in these scales’ size is effectively infinite.) But now researchers have achieved the largest range of scales yet — comparable to those found in the atmosphere — and the gaps between theory and experiment remain. The new study does show signs of universality but in a different way than existing theory predicts. As the authors point out, we’ll need new theories to explain these findings. (Image credit: D. Páscoa; research credit: C. Küchler et al.; via APS Physics)

Vortex Collisions Leave Clues to Turbulence
Vortex ring collisions have long been admired for their beauty, but they’re now shedding light on the fundamental interactions that lead to turbulence. By dying just the cores of colliding vortex rings (Image 2), researchers observed anti-symmetric perturbations that develop along each core as they interact. These are indicative of what’s known as the elliptical instability.
But the breakdown doesn’t stop there. Instead, as the elliptical instability develops, it generates a set of secondary vortex filaments that wrap around the original cores (Image 3). Just like the original vortex cores, those counter-rotating secondary filaments interact with one another, develop their own elliptical instability, and generate a set of smaller, tertiary filaments (Image 4).
What’s exciting is that this process gives us a physical mechanism for the turbulent energy cascade. Researchers have talked for decades about energy passing from large-scale eddies to smaller and smaller ones, but this work lets us actually observe that cascade in the form of smaller and smaller pairs of vortex filaments interacting. To see more, check out some of our previous posts on this work. (Image and research credit: R. McKeown et al.; via Cosmos; submitted by Ryan M. and Kam-Yung Soh)

An Introduction to Turbulence
With some help from Physics Girl and her friends, Grant Sanderson at 3Blue1Brown has a nice video introduction to turbulence, complete with neat homemade laser-sheet illuminations of turbulent flows. Grant explains some of the basics of what turbulence is (and isn’t) and gives viewers a look at the equations that govern flow – as befits a mathematics channel!
There’s also an introduction to Kolmogorov’s theorem, which, to date, has been one of the most successful theoretical approaches to understanding turbulence. It describes how energy is passed from large eddies in the flow to smaller ones, and it’s been tested extensively in the nearly 80 years since its first appearance. Just how well the theory holds, and what situations it breaks down in, are still topics of active research and debate. (Video and image credit: G. Sanderson/3Blue1Brown; submitted by Maria-Isabel C.)

Visualizing Turbulence
Turbulence, the seemingly random and chaotic state that fluids often tend toward, can be difficult to wrap one’s head around. Turn your faucet on high or pour milk into your coffee, and the flow just looks like a completely unpredictable mess. But there are important patterns to be found.These flows have many different lengthscales and timescales to them. Think of a cloud. There are very large-scale motions that are close to the size of the entire cloud, but there are also very small ones that may be only a centimeter or so in size.
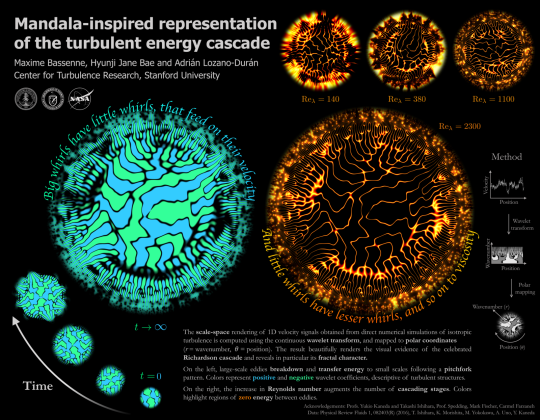
Our best understanding of turbulence so far says that energy starts out in these large scales and slowly works its way down to the smaller ones, where viscosity (essentially friction, in this case) can transform that motion into heat. Above you see a creative way to display this fact. Using data from a numerical simulation, the authors transformed velocity information into these mandala-like patterns. The center of the image represents the large lengthscales, where energy is added. Moving around the circle, like a clock’s hand does, shows different positions in space. Moving radially from the center outward takes you through different lengthscales from large to small.
Notice how the large lengthscales break into smaller and smaller ones as you move outward. The pattern looks like a set of fractal pitchforks, with each lengthscale fracturing into smaller and smaller ones as the turbulence breaks down further. There’s lots more to see in the original poster, below, but you should really click here for the glorious full-size original. The poem, by the way, is the work of physicist Lewis Richardson, who wrote it to summarize how turbulence works. (Image credit: M. Bassenne et al.)


Breaking Up Turbulence
Under most circumstances, we think about flows changing from ordered and laminar to random and turbulent. But it’s actually possible for disordered flows to become laminar again. This is what we see happening in the clip above. Upstream, the flow in this pipe is turbulent (left). Then four rotors are used to perturb the flow (center). This disrupts the turbulence and causes the flow to become laminar again downstream (right). To understand how this works, we have to talk about one of the fundamental concepts in turbulence: the energy cascade.
Turbulent flows are known for their large range of length scales. Think about a volcanic plume, for example. Some of the turbulent motions in the plume may be a hundred meters across, but there are a continuous range of smaller scales as well, all the way down to a centimeter or less in size. In a turbulent flow, energy starts at the largest scales and flows further and further down until it reaches scales small enough that viscosity can extinguish them.
That should offer a hint as to what’s happening here. The rotors are perturbing the flow, yes, but they’re also breaking the larger turbulent scales down into smaller ones. The smaller the largest lengthscales of the flow are, the more quickly their energy will decay to the smallest lengthscales where viscosity can damp them out. This is what we see here. Once the turbulent energy is concentrated at the smallest scales, viscosity damps them out and the flow returns to laminar. Check out the full video below for a cool sequence where the camera moves alongside the pipe so you can watch the turbulence fading as it moves downstream. (Image and video credit: J. Kühnen et al.)
ETA: As it turns out, there’s more going on here than I’d originally thought. Simulations show that breaking up length scales is not the primary cause of relaminarization in this case. Instead, the rotors are modifying the velocity profile across the pipe in such a way that it tends to cause the turbulence to die out. The full paper is now out in Nature Physics and on arXiv.

Turbulent Volcanic Plumes
Volcanic eruptions produce some of the largest flows on Earth. These towering ash clouds were imaged from orbit in May 2017 as an eruption began on Alaska’s Bogoslof Island. The clouds are a beautiful example of a turbulent flow. Turbulence is characterized by its many length scales. Some features in the plume are tens or hundreds of meters across, yet there are also coherent motions down at the centimeter or millimeter scale. In a turbulent flow, energy cascades from these very large scales down to the smallest ones, where viscosity is significant enough to dissipate it. This is part of the challenge of modeling turbulence; to fully describe it, you have to capture what happens at every scale. (Image credit: DigitalGlobe, via Apollo Mapping; submitted by Mark S.)

Turbulence in the Solar Wind
One of the key features of turbulent flows is that they contain many different length scales. Look at the plume from an erupting volcano, and you’ll see eddies that are hundreds of meters across as well as tiny ones on the order of millimeters. This enormous difference in scale is one of the major challenges in simulating turbulent flows. Since energy enters at the large scale and is passed to smaller and smaller scales before being dissipated at the tiniest scales of the flow, properly simulating a turbulent flow requires resolving all of these length scales. This is especially challenging for applications like the solar wind – the stream of charged particles that flows from the sun and gets diverted around the Earth by our magnetic field. The image above shows some of the turbulence in our solar wind. The structures seen in the flow range from the size of the Earth all the way to the scale of electrons! (Image credit: B. Loring, Berkeley Lab)

Volcanic Turbulence
One of the characteristics of turbulence is its large range of lengthscales. Consider the ash plume from this Japanese volcano. Some of the eddy structures are tens, if not hundreds, of meters in size, yet there is also coherence down to the scale of centimeters. In turbulence, energy cascades from these very large scales to scales small enough that viscosity can dissipate it. This is one of the great challenges in directly calculating or even simply modeling turbulence because no lengthscale can be ignore without affecting the accuracy of the results. #