FYFD

Tag: DIY fluids

  • Active Cheerios Self-Propel

    Active Cheerios Self-Propel

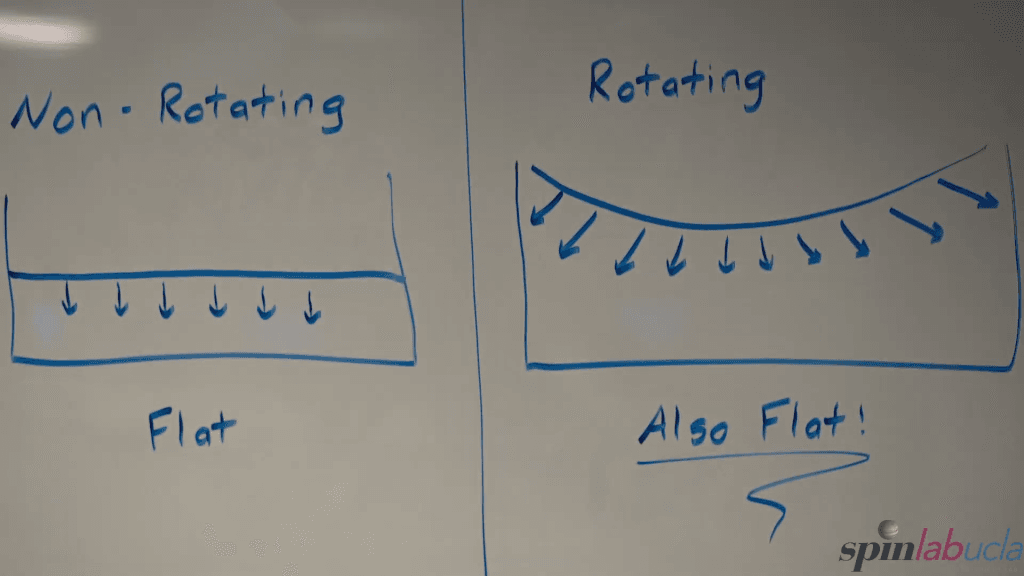
    The interface where air and water meet is a special world of surface-tension-mediated interactions. Cereal lovers are well-aware of the Cheerios effect, where lightweight O’s tend to attract one another, courtesy of their matching menisci. And those who have played with soap boats know that a gradient in surface tension causes flow. Today’s pre-print study combines these two effects to create self-propelling particle assemblies.

    The team 3D-printed particles that are a couple centimeters across and resemble a cone stuck atop a hockey puck. The lower disk area is hollow, trapping air to make the particle buoyant. The cone serves as a fuel tank, which the researchers filled with ethanol (and, in some cases, some fluorescent dye to visualize the flow). Like soap, ethanol’s lower surface tension disrupts the water’s interface and triggers a flow that pulls the particle toward areas with higher surface tension. But, unlike soap, ethanol evaporates, effectively restoring the interface’s higher surface tension over time.

    With multiple self-propelling particles on the interface, the researchers observed a rich series of interactions. Without their fuel, the Cheerios effect attracted particles to each other. But with ethanol slowly leaking out their sides, the particles repelled each other. As the ethanol ran out and evaporated, the particles would again attract. By tweaking the number and position of fuel outlets on a particle, the researchers found they could tune the particles’ attractions and motility. In addition to helping robots move and organize, their findings also make for a fun educational project. There’s a lot of room for students to play with different 3D-printed designs and fuel concentrations to make their own self-propelled particles. (Research and image credit: J. Wilt et al.; via Ars Technica)

    Fediverse Reactions
  • Featured Video Play Icon

    “Origin”

    Billowing turbulence, mushroom-like Rayleigh-Taylor instabilities, and spreading flows abound in Vadim Sherbakov’s “Origin.” The short film takes a macro looks at fluids — inks, alcohols, soaps, and other household liquids. It was filmed entirely on a DJI Pocket 2, a rather small, stabilized pocket camera. It’s a testament to what you can achieve with some experimentation and relatively inexpensive equipment. (Video and image credit: V. Sherbakov)

  • Featured Video Play Icon

    Convection in Action

    We’re surrounded daily by convection — a buoyancy-driven flow — but most of the time it’s invisible to us. In this video, Steve Mould shows off what convection really looks like with some of his excellent tabletop demos. The first half of the video gives profile views of turbulent convection, with chaotic and unsteady patterns. When he switches to oil instead of water, the higher viscosity (and lower Reynolds number) offer a more structured, laminar look. And finally, he shows a little non-temperature-dependent convection with a mixture of Tia Maria and cream, which convects due to evaporation changing the density. (Image and video credit: S. Mould; submitted by Eric W.)

  • Featured Video Play Icon

    Serpents and Ouroboros

    Beads of condensation on a cooling, oil-slicked surface have a dance all their own in this video. Large droplets gobble up their fellows as they follow serpentine paths; each new droplet donates its interfacial energy to feed the larger drop’s kinetic energy. Eventually, the big drops switch to a circular path, like an ouroboros, the tail-eating serpent of mythology. This transition happens due to the oil shifted by the dancing droplets. You can recreate the effect at home by rubbing a thin layer of oil over glass and setting it atop a hot mug of your favorite beverage. (Video and image credit: M. Lin et al.; research credit: M. Lin et al.)

  • Food-Based Fluid Dynamics

    Food-Based Fluid Dynamics

    The kitchen is a rich source of fluid physics. From cocktails to coffee, from crepes to tempura, food is full of physics. In fact, it’s not hard to relate almost any fluid phenomenon you can imagine to something that goes on in the kitchen. That’s why scientists managed to write a 77-page review article of culinary fluid dynamics. It’s even structured after a menu, carrying readers from the kitchen sink and cocktails all the way through a meal and the process of washing up afterward! (Image credit: top – S. Hsu, others – A. Mathijssen et al.; research credit: A. Mathijssen et al.; via APS Physics)

  • Stopping a Bottle’s Bounce

    Stopping a Bottle’s Bounce

    A few years ago, the Internet was abuzz with water bottle flips. Experimentalists are still looking at how they can arrest a partially fluid-filled container’s bounce, but now they’re rotating the bottles vertically rather than flipping them end-over-end. Their work shows that faster rotating bottles have little to no bounce after impacting a surface.

    This image sequence shows how water in a rotating bottle moves during its fall (top row) and after impact (bottom row). Water climbs the walls during the fall, creating a shell of fluid that, after impact, forms a central jet that arrests the bottle's momentum.
    This image sequence shows how water in a rotating bottle moves during its fall (top row) and after impact (bottom row). Water climbs the walls during the fall, creating a shell of fluid that, after impact, forms a central jet that arrests the bottle’s momentum.

    The reason for this is visible in the image sequence above, which shows a falling bottle (top row) and the aftermath of its impact (bottom row). When the bottle rotates and falls, water climbs up the sides of the bottle, forming a shell. On impact, the water collapses, forming a central jet that shoots up the middle of the bottle, expending momentum that would otherwise go into a bounce. It’s a bit like the water is stomping the landing.

    The authors hope their observations will be useful in fluid transport, but they also note that this bit of physics is easily recreated at home with a partially-filled water bottle. (Image and research credit: K. Andrade et al.; via APS Physics)

  • Featured Video Play Icon

    DIY Superwalking Droplets

    Over the past few years, we’ve seen lots of research in walking droplets, especially as hydrodynamic quantum analogs. But did you know you can replicate this set-up at home and play with it yourself? This video gives an overview of the equipment you’ll need and a simple procedure to follow to get it up and running. From there, your imagination is the limit! (Image and video credit: R. Valani)

  • Featured Video Play Icon

    Aerated Faucets

    So much goes on in our daily lives that we never see. But with the power of the smartphones in our pockets, we can catch more than ever before, as illustrated in this video. Here a researcher uses the standard “slo-mo” (240 fps) video mode on a smartphone to look at the flow from a typical kitchen faucet. Household faucets often have an aerator that adds air bubbles to the flow, something that’s particularly visible in slow motion at high flow rates. What you can see depends on more than just the frame rate, though. Without strong illumination — provided in this case by sunlight — you could easily miss the cloud of droplets ejected by the faucet. (Image and video credit: M. Mungal)

  • Featured Video Play Icon

    Pop-Pop Boats

    I confess I’ve never heard of the pop-pop boat toys Steve Mould uses in this video. They feature a tank filled with water and a small source of heat in the form of a tea light candle. Together, these features generate propulsion and a distinctive popping sound from the toy. As he is wont to, Mould explains the physics behind the toy using a transparent version to show the water/steam oscillations that drive the boat. Having watched, I have to say that this set-up seems ready made for an undergrad fluids class and a control volume analysis! (Image and video credit: S. Mould)

  • Featured Video Play Icon

    Self-Stopping Leaks

    A leak can actually stop itself, as shown in this video. To demonstrate, the team used a tube pierced with a small hole. When filled, water initially shoots out the hole in a jet. The pressure driving the jet comes from the weight of the fluid sitting above the hole. As the water level drops, the pressure drops, causing the jet to sag and eventually form a rivulet that wets the side of the tube. As the water level and driving pressure continue to fall, the rivulet breaks up into discrete droplets, whose exact behavior depends on how hydrophobic the tube is. Eventually, a final droplet forms a cap over the hole and the leak stops. At this point, the flow’s driving pressure is smaller than the pressure formed by the curvature of the capping droplet. (Image and video credit: C. Tally et al.)