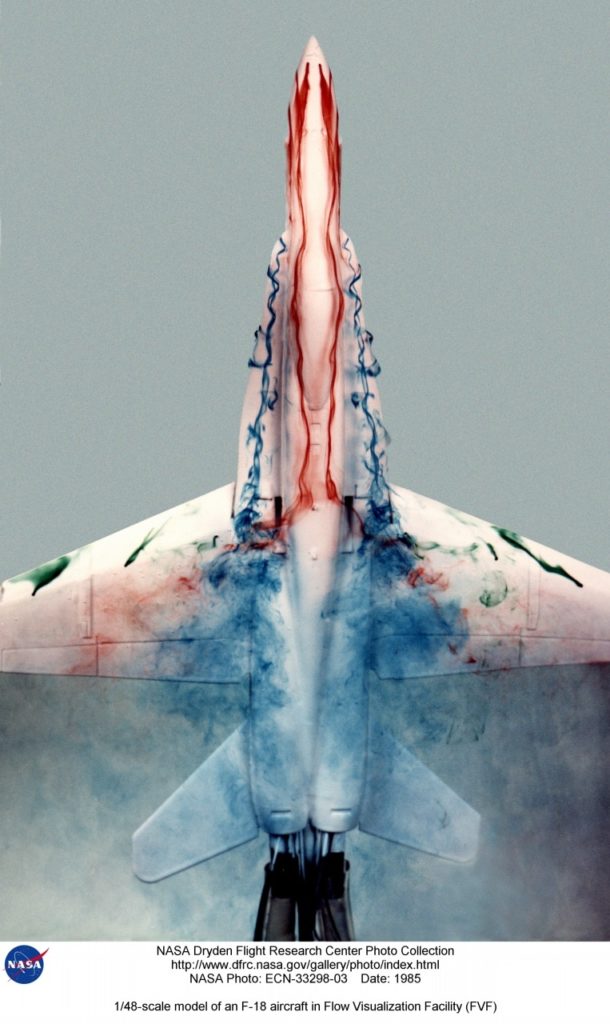
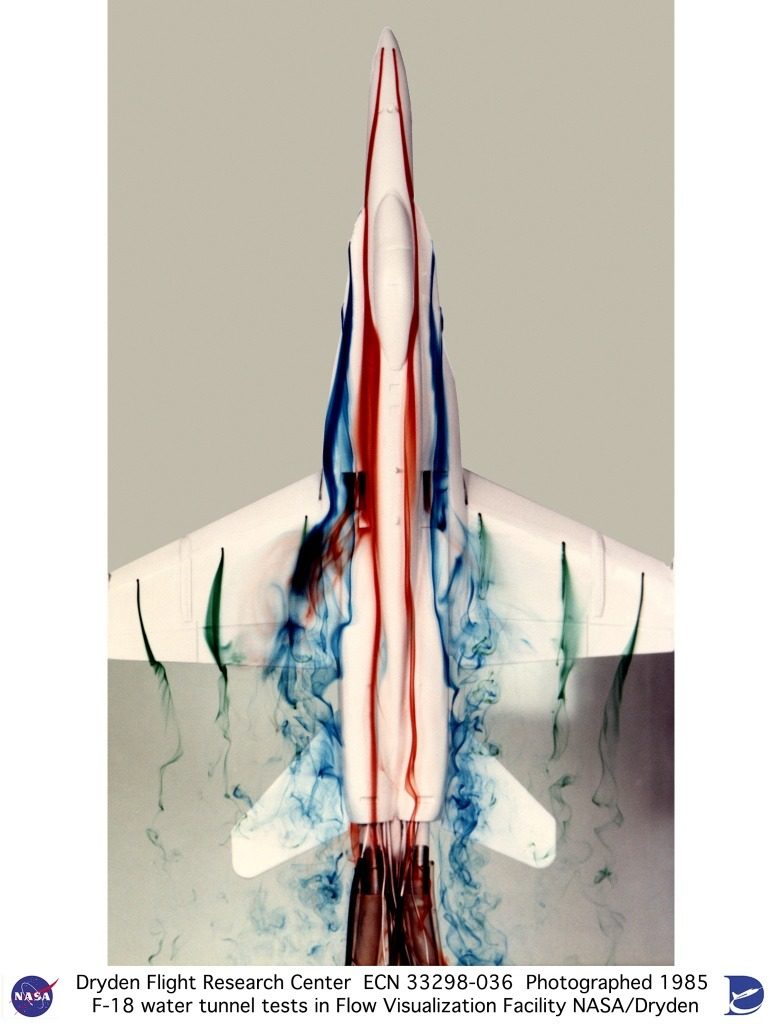
Water tunnels are useful tools for determining aerodynamic characteristics of aircraft, such as this F-18 model placed in the NASA Dryden Flow Visualization Facility. By matching the Reynolds number of the model in the water tunnel to that of the full-scale aircraft in air, engineers can observe flow around the aircraft inside the laboratory. This similarity of flows is a powerful design tool. Here dye introduced along the nose, wings, and fuselage traces streamlines around the F-18, revealing areas of turbulence at different flight conditions.
Tag: Reynolds number
Reader Question: Creeping Flow
[original media no longer available]
David asks:
I’m taking an undergraduate fluid dynamics course, and I’m having trouble understanding what a Creeping Flow exactly is. The only thing I understand about that is that the Re should be 0 or close to 0 for the flow… Could you post an example of a creeping flow please? Thank you!
Absolutely! Creeping flow, also called Stokes flow, is, like you said, a very low Reynolds number flow. It would be hard to say that the Reynolds number is zero because that would seem to imply no flow at all. Think of it instead as a Reynolds number much, much less than one. When the Reynolds number is very low, it means that viscous forces are dominating the flow. The video above shows creeping flow around a cylinder; notice how the streamlines stay attached all the way around the surface of the cylinder. There’s no separation, no turbulent wake, no von Karman vortex street. Viscosity is so dominant here that it’s damped out all of that inertial diffusion of momentum.
We’ve posted some other great examples of creeping flow, as well, though not by that name. There are the reversible laminar flow demos and various experiments in Hele-Shaw cells, all of which qualify as creeping flow because of their highly viscous nature. If you have the time, there’s also a great instructional video from the 1960s called “Low Reynolds Number Flow” (Parts 1, 2, 3, 4) starring G. I. Taylor (a famous fluid dynamicist) that is full of one demo after another.

Volcanic Ash Plume
Video footage of Iceland’s Grimsvotn volcano erupting shows a massive turbulent plume of ash. The largest scales of the plume are of the order of hundreds, if not thousands of meters, and the eddies of the plume appear to move very slowly, especially far from the base. According to Kolmogorov, however, at the smallest scales of the flow (< 1 mm), the turbulent motions are isotropic. No one has been able to achieve Reynolds numbers high enough to fully prove or disprove Kolmogorov’s hypothesis, but natural events like volcanic eruptions produce some of the largest Reynolds numbers on earth. (See also: interview with videographer; via Gizmodo, jshoer)
Reader Question: Froude vs. Reynolds
@spooferbarnabas asks: I was wondering what the difference is between Froude’s number and Reynold’s number? they seem very similar
Fluid dynamicists often use nondimensional numbers to characterize different flows because it’s possible to find similarity in their behaviors this way. The Reynolds number is the most common of these dimensionless numbers and is equal to (fluid density)*(mean fluid velocity)*(characteristic length)/(fluid dynamic viscosity). The Reynolds number is considered a ratio of total momentum (or inertial forces) to the molecular momentum (or viscous forces). A small Reynolds number indicates a flow dominated by viscosity; whereas a flow with a large Reynolds number is considered one where viscous forces have little effect.
The Froude number, in contrast, focuses on resistance to flow caused by gravitational effects, not molecular effects. It is defined as (mean fluid velocity)/(characteristic wave propagation velocity). Initially, it was developed to describe the resistance of a model floating in water when towed at a given speed. As the boat’s hull moves through the water, it creates a wave that travels forward (and backward in the form of the wake), carrying information about the boat–much like pressure waves travel before and behind a subsonic aircraft. The speed of the wave created by the boat depends on gravity (see shallow water waves). The closer the boat’s speed comes to the water wave’s speed, the greater the resistance the boat experiences. In this respect, the Froude number is actually analogous to the Mach number in compressible fluids.
I hope that helps explain some of the differences!