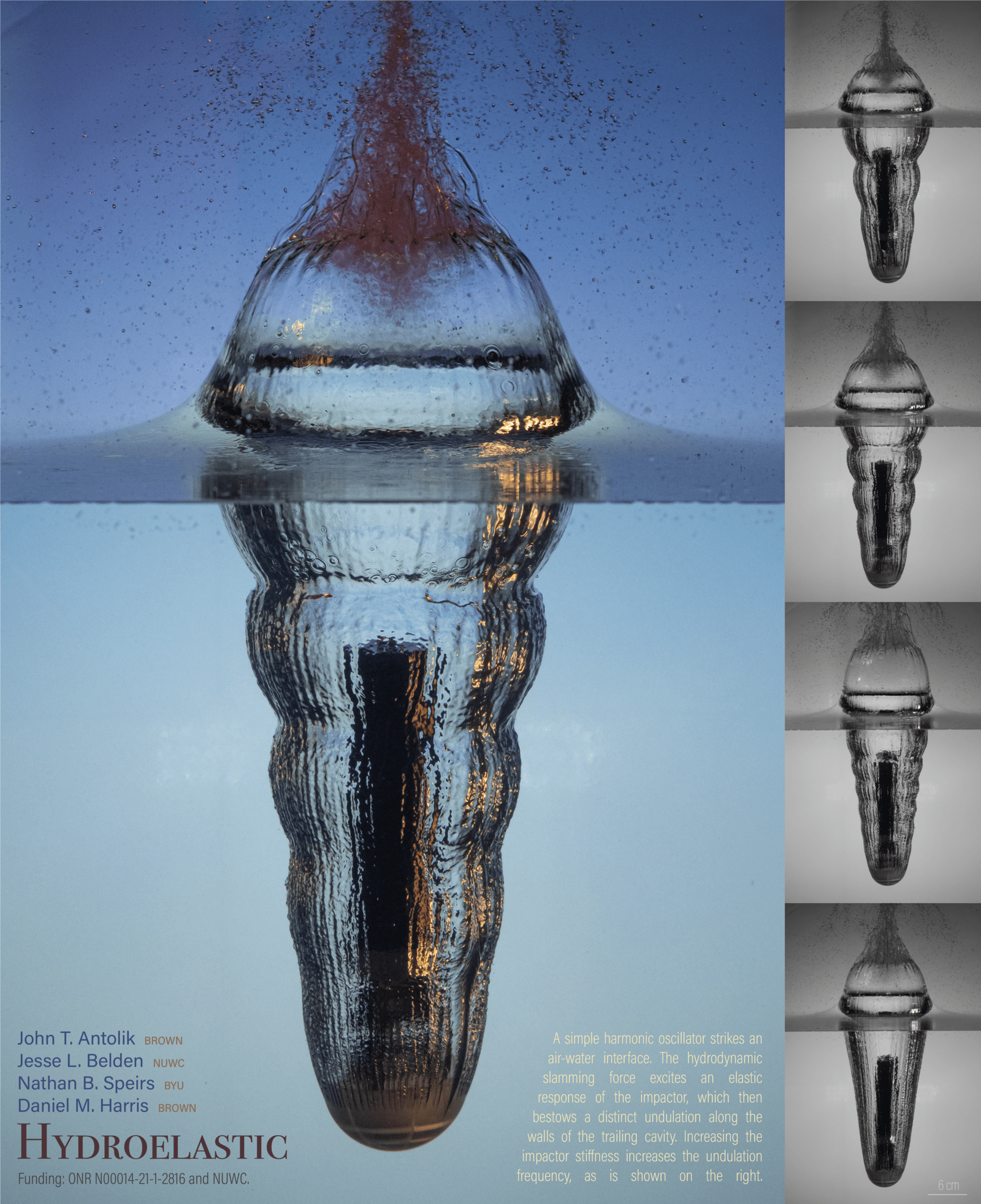When objects impact water with enough speed, they create a smooth-walled, air-filled cavity around and behind them. Here, the impacting object is one with some give, like a spring. The initial impact squishes the object, setting it to oscillating along its length. The result is a wavy cavity. The stiffer the object, the more frequent the waves. (Image credit: J. Antolik et al.)
Tag: oscillation

A Game of Toss
Over the past few years, we’ve seen lots of droplets bouncing and walking on waves. But today’s example is a little different. In this set-up, the wave is a large standing wave that sloshes from side-to-side in a narrow container. As it does, the wave catches and tosses a large ~3mm water droplet. The system is surprisingly stable, with this game of catch lasting for tens of thousands of cycles and up to 90 minutes before the droplet coalesces. The researchers found that, if the droplet tries to wander from its spot, the oscillating surface wave corrects it, guiding the droplet back to the optimal position. (Image and research credit: C. Sandivari et al.; via APS Physics; submitted by Kam-Yung Soh)

In a Box, Shaken
Tidal areas experience lots of oscillating, back-and-forth flow that builds up patterns in the sand below. In this experiment, researchers investigate a similar situation by filling a box with water and spherical particles, then shaking the box from side-to-side. Inside the box, the particles line up in chains that are perpendicular to the direction of oscillation (think sand ripples parallel to a shoreline). In this simplified system, the team can then look at what forces align the particles, how defects in the pattern shift, and what happens when the oscillation gets bigger. (Image and video credit: T. van Overveld et al.)

Perturbations
At first glance, today’s video appears to have little to do with fluid dynamics since it’s a demonstration of interactions between magnets. But for those who’ve delved into the mathematics of fluid dynamics — especially subjects like perturbation theory — there’s a lot to appreciate here. In the video, we see systems of magnets constructed and then manipulated, often by moving a single magnet and watching how the rest respond. Visually, this demonstrates how disturbances move in complex, interconnected damped systems. The auditory component — definitely turn the sound on for this video — is an extra layer of fluids-related goodness that also shows how reconfiguring a system changes its resonant frequencies. (Image and video credit: Magnetic Tricks and Magnetic Games; via Colossal)

Pop-Pop Boats
I confess I’ve never heard of the pop-pop boat toys Steve Mould uses in this video. They feature a tank filled with water and a small source of heat in the form of a tea light candle. Together, these features generate propulsion and a distinctive popping sound from the toy. As he is wont to, Mould explains the physics behind the toy using a transparent version to show the water/steam oscillations that drive the boat. Having watched, I have to say that this set-up seems ready made for an undergrad fluids class and a control volume analysis! (Image and video credit: S. Mould)

Vortex Arms
A fixed cylinder will shed alternating vortices in its wake, but one allowed to oscillate forward and backward in the flow instead sheds simultaneous vortices. The shape of the wake still depends on the flow’s velocity. At low flow speeds, the two vortices are the same size when they shed. At higher velocities, the two vortices still shed simultaneously, but one will be large while the other is small. The larger vortex moves faster and travels downstream, but the smaller, slower vortex drifts inward. In the next shedding cycle, the small and large vortices switch positions, creating alternating symmetric shedding. (Image and video credit: P. Boersma et al.)

Leidenfrost Stars
Atop a very hot surface, liquids can instantly vaporize, leaving a drop levitating on a layer of its own vapor. These Leidenfrost droplets demonstrate all kinds of interesting behaviors, including self-propulsion, explosion, and star-shaped oscillations, like those above. The oscillation is driven by feedback between the drop and its vapor layer.
Interestingly, the drops are capable of sustaining more than one mode of oscillation at once, as seen above. The obvious mode (m=5) corresponds to the 5 star-like points pushing out on the drop. But notice that the drop is also stretching into an oval shape that moves up and down, back and forth. This is the second mode (m=2) present. It moves slower than the m=5 mode, completing a cycle only once for every four cycles the other has. (Image and research credit: J. Bergen et al.)

Settling in Straws
At some point in your life, you’ve probably stuck your finger over the end of a straw and used it to pick up the liquid you’re drinking. If you lift the straw so that the end is still in your drink and remove your finger from the top, the liquid level in the straw will drop, then bounce up and down a couple times before it settles. This is what we see happen in the series of snapshots in the top image. Eventually, the liquid level settles at its equilibrium position, marked by the red arrow at the far right.
The liquid has to bounce before settling because capillary forces and the liquid’s inertia are battling it out moment by moment. Just how long the rebound takes depends on the initial height of the fluid and the depth the straw is immersed at, but it doesn’t depend on the fluid’s viscosity. Lower viscosity fluids do sometimes have a neat jet (bottom image) that forms at the immersed end of the straw, though. (Image and research credit: J. Marston et al.)

Shaping and Levitating Droplets
Opposing ultrasonic speakers can be used to trap and levitate droplets against gravity using acoustic pressure. Changes to field strength can do things like bring separate objects together or flatten droplets. The squished shape of the droplet is the result of a balance between acoustic pressure trying to flatten the drop and surface tension, which tries to pull the drop into a sphere. If the acoustic field strength changes with a frequency that is a harmonic of the drop’s resonant frequency, the drop will oscillate in a star-like shape dependent on the harmonic. The video above demonstrates this for many harmonic frequencies. It also shows how alterations to the drop’s surface tension (by adding water at 2:19) can trigger the instability. Finally, if the field strength is increased even further, the drop’s behavior becomes chaotic as the acoustic pressure overwhelms surface tension’s ability to hold the drop together. Like all of this week’s videos, this video is a submission to the 2103 Gallery of Fluid Motion. (Video credit: W. Ran and S. Fredericks)

Pendulum Soap Flow Viz
Soap films are a handy way to create nearly two-dimensional flow fields. Previously we’ve seen them used to show wake structures of pitching foils, flapping flags, and multiple bodies. In this video, we see the dynamics of a pendulum in a soap film. Initially its length is quite long, and the ring end of the pendulum bobs side-to-side in a figure-8 motion. There are two rotational effects here: one is the standard oscillation of a pendulum about its pivot, the other is the rotation of the pendulum’s ring about its attachment point. Interestingly, they have the same frequency. The major destabilizing force for the pendulum is the periodic shedding of vortices we see off the ring. By shortening the pendulum length, the pendulum’s behavior shifts; first it loses the stationary node in its string. Eventually, the string becomes so short that the pendulum no longer oscillates. (Video credit: M. Bandi et al.)