FYFD

Tag: bernoulli

  • Featured Video Play Icon

    How Gas Pump Nozzles Work

    Ever wonder how a gas pump shuts off when the tank is full? You might guess that there’s a sophisticated electronic sensor hidden in there. But there isn’t! Gas pumps use an entirely mechanical technique to sense a full tank and shut off flow, as Steve Mould demonstrates in this video.

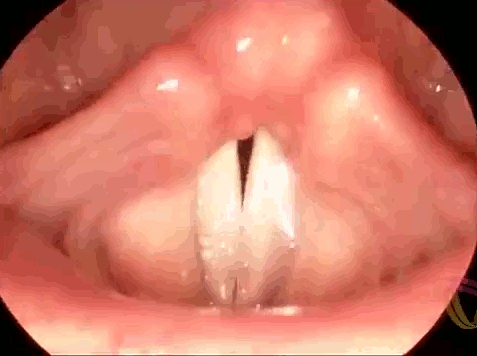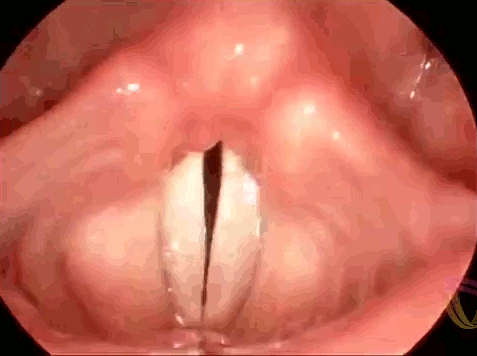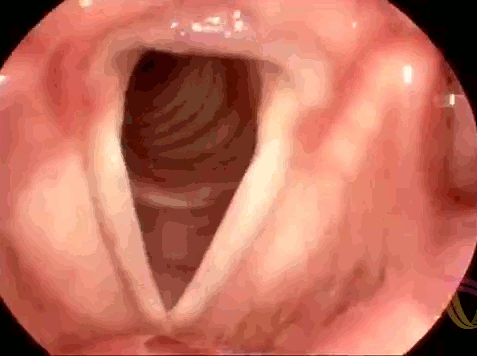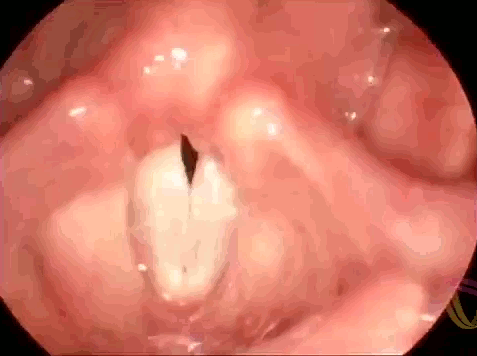
    There are two key components — one fluid mechanical and one based on mechanical linkages — inside the handle. The part that senses a full tank is a Venturi tube, shown in Image 2. The top section of the Venturi tube contains a constriction, where (incompressible) flow is forced to speed up. That increase in speed creates a drop in pressure, which is reflected by the movement of the water in the curved tube below the constriction.

    Notice that when there’s no flow through the top tube, the water level is equal on either side of the lower, curved tube. That means that the outside air pressure (connected to the short arm) equals the pressure in the constriction (connected to the long arm). When air is flowing through the constriction, the water level shifts. The water in the short arm gets pushed down while the water in the long arm gets sucked up. That change means that the air pressure outside the tube is now higher than pressure in the constriction.

    I’ll let Steve explain what that means for the gas pump! (Image and video credit: S. Mould)

  • Featured Video Play Icon

    Lift Over Wings

    One of the most vexing topics for fluid dynamicists and their audiences is the subject of how wings generate lift. As discussed in the video above, there are a number of common but flawed explanations for this. Perhaps the most common one argues that the shape of the wing requires air moving over the top to move farther in the same amount of time, therefore moving faster. The flaw here, as my advisor used to say, is that there is no Conservation of Who-You-Were-Sitting-Next-To-When-You-Started. Nothing requires that air moving over the top and bottom of a wing meet up again. In fact, the air moving over the top of the wing outpaces air moving underneath it.

    In the Sixty Symbols video, the conclusion presented is that any complete explanation requires use of three conservation principles: mass, momentum, and energy. In essence, though, this is like saying that airplanes fly because the Navier-Stokes equations say they do. It’s not a terribly satisfying answer to someone uninterested in the mathematics.

    Part of the reason that so many explanations exist – here’s one the video didn’t touch on using circulation – is that no one has presented a simple, intuitive, and complete explanation. This is not to say that we don’t understand lift on fixed wings – we do! It’s just tough to simplify without oversimplifying.

    Here’s the bottom line, though: the shape of the wing forces air moving around it to change direction and move downward. By Newton’s 3rd law (equal and opposite reactions), that means the air pushes the wing up, thereby creating lift. (Video credit: Sixty Symbols)

  • Venturi Splashes

    Venturi Splashes

    Diving can generate some remarkable splashes. Here researchers explore the splashes from a wedge-shaped impactor. At high speeds, they found that the splash sheet pushed out by the wedge curls back on itself and accelerates sharply downward to “slap” the water surface (top). Studying the air flow around the splash sheet reveals some of the dynamics driving the slap (bottom). The splash sheet quickly develops a kink that grows as the sheet expands. This creates a constriction that accelerates flow on the underside of the sheet. That higher velocity flow means a low pressure inside the constriction, which pulls the thin sheet down rapidly, making it slap the surface. For more, check out the full video. (Image and research credit: T. Xiao et al., source)

  • The Kamifusen

    The Kamifusen

    The kamifusen is a traditional Japanese toy made of colorful paper. It resembles a beach ball, but unlike that toy, the kamifusen has an open hole at one end. Given that hole, one might expect the toy to deflate when struck, but the opposite is true – a deflated kamifusen inflates itself when bounced. The key to this counter-intuitive behavior comes from a combination of fluid dynamics and solid mechanics.

    When the kamifusen bounces off a player’s hand, it is compressed, which increases pressure inside the toy and forces some air out. Elastic waves rebound through the ball’s paper walls, much like seismic waves traveling outward from an earthquake. Those waves re-expand the toy’s walls, dropping the interior pressure and pulling air in from the outside. Although the pressure spike from impact is larger, its duration is short compared to the low pressure generated by the subsequent elastic waves. As a result, more air flows into the toy than is knocked out, and so the kamifusen inflates. For more, check out this explanation at Physics Today.  (Image and research credit: I. Fukumori, source; submitted by E. van Andel)

  • Inside Singing

    Inside Singing

    These are the vocal folds of a woman singing. Human speech (and song) results from interactions between elastic muscles and aerodynamics. As we exhale, the vocal folds are initially pushed apart, then the flow of air moving past creates low pressure (via the Bernoulli effect) that helps pull the folds together. As the folds close, high pressure again forms to force them open. This sets a cycle of oscillation or vibration that produces sound. To change the pitch of the sounds we create, we can lengthen or shorten the vocal folds or change their tension. In this respect, they behave somewhat similarly to the strings of a musical instrument. If you’d like to admire more vocal folds in action, check out this endoscopic video for four singers performing together. (Image credit: LinguaHealth, source)

  • Featured Video Play Icon

    Crash Course Fluids

    Crash Course Physics returns to the subject of fluids with their video on fluid dynamics. They stick with ideal fluids (i.e. incompressible, inviscid, laminar flows) for simplicity and cover some of the basics by discussing conservation of mass (also called continuity) and a simple form of Bernoulli’s equation. Despite keeping things basic, the video does a nice job introducing these topics; I especially like that they explain Bernoulli’s equation as a form of conservation of energy. Sometimes it’s easy to let the terminology in fluid dynamics mask the fact that the equations we use are just alternative forms of the classical equations for conserving mass, momentum, and energy. As with their fluids at rest video, the information is densely packed, so expect to pause and rewind. (Video credit: Crash Course)

  • Prairie Dog Physics

    Prairie Dog Physics

    One challenge facing burrowing mammals is ensuring sufficient oxygen within their den. Prairie dogs achieve this with a clever use of Bernoulli’s principle. They build multiple entrances to their tunnels. One of them, labeled as Entrance A above, is built with a raised mound of dirt, while the other, Entrance B, is not. The raised mound creates an obstacle for the wind to move around, which increases the wind velocity at Entrance A compared to the normal wind speed at Entrance B. From Bernoulli’s principle, we know that a higher velocity means a lower pressure, so there is a decreasing pressure gradient through the tunnel from Entrance B to Entrance A. That favorable pressure gradient pulls fresh air through the prairie dog tunnels, allowing the colony to breathe easy. (Image credits: N. Sharp; original prairie dog photos by jinterwas and J. Kubina; final images shared under Creative Commons; research credit: S. Vogel et al.; h/t to Chris R.)

  • Meander from Above

    Meander from Above

    This photo of the Amazon River taken by Astronaut Tim Kopra reveals the many meandering changes of the river’s course. Left untouched by human intervention, rivers tend to get more curvy, or sinuous, over time, simply due to fluid dynamics. Imagine a single bend in a river. Due to conservation of angular momentum, water flows faster around the inside curve of the bend than the outside – just like an ice skater spins faster with her arms pulled in. From Bernoulli’s principle, we know there is an accompanying pressure gradient caused by this velocity difference – with higher pressure near the outer bank and lower pressure on the inner one. This pressure gradient is what guides the water around the bend, keeping the bulk of the fluid moving downstream rather than bending toward either bank.

    At the bottom of the river, though, viscosity slows the water down due to the influence of the ground. This slower water, still subject to the same pressure gradient as the rest of the river, cannot maintain its course going downstream. Instead, it gets pushed from the outer bank toward the inner bank in what’s known as a secondary flow. This secondary flow carries sediment away from the outer bank and deposits it on the inner bank, which, over time, makes the river bend more and more pronounced. (Image credit: T. Kopra/NASA; submitted by jshoer)

    Do you enjoy FYFD and want to help support it? Then please consider becoming a patron!

  • Featured Video Play Icon

    “En Plein Vol”

    Artist Antoine Terrieux’s “En Plein Vol” exhibit shows off the power of hair dryers. Parts of the exhibit, like the floating ball at 0:16, rely on Bernoulli’s principle and the moving stream of air the dryers generate. Others, like the smoke tornado at 0:39 or the (suspended) paper airplane at 0:56, use the hair dryers to generate vorticity essential to the installation. It’s a neat concept and very well executed. (Video credit: A. Terrieux; via io9; submitted by Joseph S. and Eliza M.)

  • Frisbee Physics

    Frisbee Physics

    Frisbees are a popular summertime toy, but they involve some pretty neat physics, too. Two key ingredients to their long flight times are their lift generation and spin. A frisbee in flight behaves very much like a wing, generating lift by flying at an angle of attack. This angle of attack and the curvature of the disk rim cause air to accelerate over the top of the leading edge. Airflow over the top of the disk is faster than that across the bottom;  thus, pressure is lower over the top of the frisbee and lift is generated. Aerodynamic lift and drag aren’t enough to keep the frisbee aloft long, though. Spin matters, too. If the frisbee is launched without spin, gravity acts on it through its center of mass, but lift and drag act through a point off-center because lift tends to be higher on the front of the disk than the back. This offset between gravitational forces and aerodynamic forces creates a torque that tends to flip the frisbee. By spinning the frisbee, the thrower gives it a high angular momentum acting about its spin axis. Now instead of flipping the disk, the torque caused by the offset forces just tips the angular momentum vector slightly. Physically, this is known as spin stabilization or gyroscopic stability. Tomorrow we’ll take a closer look at airflow over the frisbee.  (Image credit: A. Leibel and C. Pugh, source video; recommended papers by: V. Morrison and R. Lorentz)