FYFD

Tag: self-organization

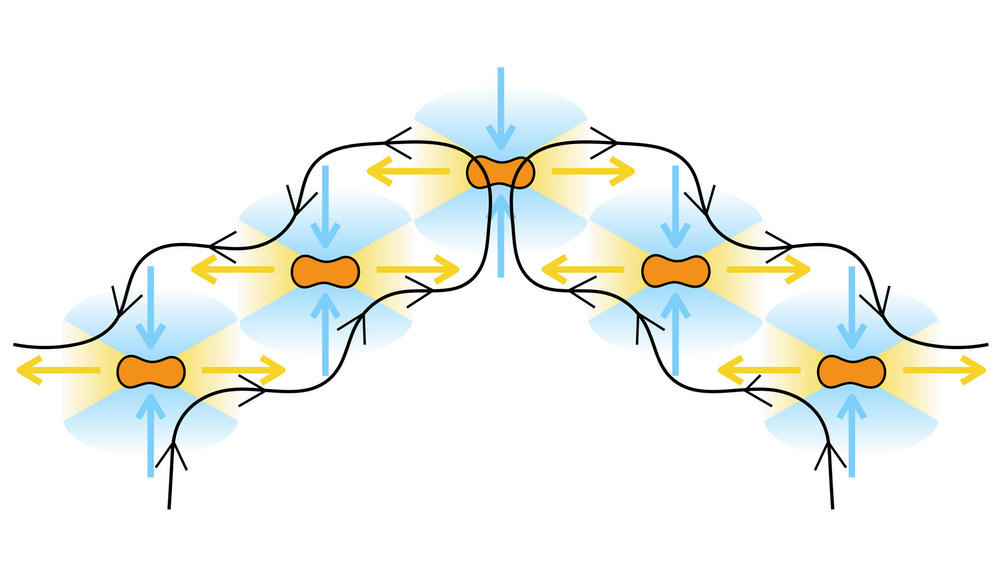
  • Forming Zigzags

    Forming Zigzags

    Scientists are fascinated by the organized patterns that can emerge from non-living systems. Here, researchers study micron-sized magnetic particles, immersed in a viscoelastic fluid and subjected to an oscillating magnetic field. The peanut-shaped particles roll around their long axis and assemble to form millimeter-sized bands of zigzags. These patterns, the researchers found, do not depend on the particles’ specific shape or on the details of the applied magnetic field. Instead, the zigzags depend only on the symmetry of the flow generated around each particle. In their system, illustrated above, each particle pushed fluid away along their long axis and drew in fluid toward their waist; as a result, particle pairs would attract or repel, depending on their relative orientation. That interparticle force ultimately caused the particles to self-organize into zigzags. (Image, video, and research credit: G. Junot et al.; via APS Physics)

    This sped-up animation shows the zig-zag pattern that the particles self-organization into.
    This sped-up animation shows the zigzag pattern that the particles self-organization into.
  • Hedgehogs Atop Waves

    Hedgehogs Atop Waves

    Since Michael Faraday, scientists have watched the curious patterns that form in a vibrating liquid. By adding floating particles to such a system, researchers have discovered spiky, hedgehog-like shapes that form near the surface. At low amplitudes, the surface patterns resemble the typical smooth rounded lobes one would expect, but as the wave amplitude increases, spikes form in the tracers, driven by the motion of the waves. (Image and research credit: H. Alarcón et al.; via APS Physics)

  • Self-Assembly Under Stratification

    Self-Assembly Under Stratification

    Sometimes mistakes lead to great discoveries. After leaving a failed outreach demo overnight, researchers discovered a new mechanism for self-assembling particles. In the initial set-up, a layer of fresh water is poured atop a layer of denser, saltier water. This creates what’s known as a stably stratified fluid, with progressively denser mixtures of salt water as one moves downward. If you pour in particles of an intermediate density (heavier than fresh water and lighter than salt water), they’ll form a layer at one height, and, if you wait overnight, those particles will slowly form a disk-like raft.

    A spheroidal particle causes attractive flow at its equator and repulsive flow at its poles.

    This self-assembly is driven by fluid dynamics — not by any attraction between the particles. Because the particles are unable to absorb salt, their boundaries distort the concentration gradients in the surrounding fluid. This generates subtle currents at the particle boundaries, like in the picture above, where flow moves toward the particle at the equator and away at the poles. Larger particle clusters generate stronger flows, allowing them to attract even more particles.

    Although the speeds involved are quite slow, this mechanism may play an important role in nature, where stratified flows are common. The researchers speculate, for example, that the effect could be important in the clustering of microplastics in the ocean. (Image and research credit: R. Camassa et al.; see also R. McLaughlin; submitted by Kam-Yung Soh)

  • Floccing Particles

    Floccing Particles

    Adding particles to a viscous fluid can create unexpected complications, thanks to the interplay of fluid and solid interactions. Here we see a dilute mixture of dark spherical particles suspended in a layer of fluid cushioned between the walls of an inner and outer cylinder. Initially, the particles are evenly distributed, but when the inner cylinder begins to rotate, it shears the fluid layer. Hydrodynamic forces assemble the particles together into loose conglomerates known as flocs. Once the particles form these log-like shapes, they remain stable thanks to the balance between viscous drag on particles and the attractive forces that pull particles toward one another. (Image and research credit: Z. Varga et al.; submitted by Thibaut D.)

  • Order in Chaos

    Order in Chaos

    Although turbulent flow is chaotic, it’s not completely disordered. In fact, order can emerge from turbulence, though exactly how this happens has been a long-enduring mystery. Take the animations above. They show the flow that develops between two plates moving in opposite direction that are separated by a small gap. (The formal name for this is planar Couette flow.) The visualization is taken in a plane at a fixed height between the plates.

    Initially (top), the flow shows narrow bands of turbulence, shown in green, separated by calmer, laminar zones in black. As time passes, these areas of laminar and turbulent flow self-organize, eventually forming diagonal stripes that are much longer than the gap between plates (bottom), the natural length-scale we would expect to see in the flow. Researchers have wondered for years why these distinctive stripes form. What sets their spacing, and why are they along diagonals?

    To answer those questions, researchers explored the full Navier-Stokes equations, searching for equilibrium solutions that resemble the striped patterns seen in experiments and simulation. And for the first time, they’ve found a mathematical solution that matches. What the work shows is that the pattern emerges naturally from the equations; in fact, given the characteristics of the solution, the researchers found that many disturbances should lead to this result, which explains why the pattern appears so frequently. (Image and research credit: F. Reetz et al., source; via phys.org; submitted by Kam-Yung Soh)

  • PyeongChang 2018: Moguls

    PyeongChang 2018: Moguls

    Moguls are bump-like snow mounds featured in freestyle skiing competitions and also frequently found on recreational ski courses. Although competition runs are man-made, most mogul fields form naturally on their own. As skiiers and snowboarders carve S-shaped paths down the slope, their skis and snowboards remove snow during sharp turns and deposit it further downhill. Over a surprisingly short amount of time, these random, uncoordinated actions form bumps large enough that they force skiers and snowboarders to begin turning on the downhill side of the bump. That action continues to carve out snow on the uphill side and deposit it downhill, effectively causing the downhill bumps to migrate uphill, as seen in the timelapse animation below. As more moguls form, their motion organizes them into a checkerboard-pattern that moves in lockstep. Observations show that mogul fields can move about 10 meters uphill over the course of a season. Seemingly, the only way to prevent mogul formation on steep slopes is to regularly groom them back to a flat state! (Image credits: J. Gruber/USA Today; J. Huet; D. Bahr; research credit:  D. Bahr et al.)

    image
  • Sand Ripples in Tidal Flats

    Sand Ripples in Tidal Flats

    Sand, winds, and waves can interact to form remarkable and complex patterns. These sand ripples from the tidal flats of Cape Cod are a testament to such interactions. When a fluid like air or water flows over a flat bed of sand, it can shear and lift grains of sand, moving them to a new location. Very quickly, turbulence within the flow disturbs the initially smooth surface and begins to form the wavelike crests we see. Because the change in surface shape alters the nearby air or water flow, there is a trend toward self-organization and persistence. In other words, once the ripples form, they’re reinforced by their effect on the wind or water that formed them. Once rippled, the surface does not tend to smooth back out. (Image credit: N. Sharp; research credit: F. Sotiropoulos and  A. Khosronejad)