FYFD

Tag: q&a

  • Reader Question: Drafting in Time Trials

    Reader Question: Drafting in Time Trials

    In a comment on this recent post regarding drafting advantages to a leader, reader fey-ruz asks:

    in cycling, team follow cars are required to maintain a minimum distance from their riders during time trials for this very reason (although i imagine the effects in that context are much smaller and dependent on the conditions, esp the wind speed, direction, and strength). FYFD, is there a simple way to understand where this upstream influence comes from? or a specific term in the navier-stokes equations that it results from?

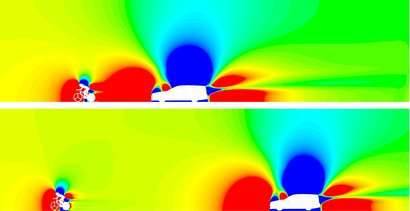
    Cars following riders during a time trial can actually make a huge difference! One study from a couple of years ago estimated that a car following a rider in a short (13.8 km) time trial could take 6 seconds off the rider’s time. The images up top show a simulation from that study with a car following at 5 meters versus 10 meters. The colors indicate the pressure field around the car and rider. Red is high pressure, blue is low pressure. Both the car and the rider have high pressure in front of them; you can think of this as a result of them pushing the air in front of them.

    A large part of the rider’s drag comes from the difference in pressure ahead and behind them. (For a look at flow around a cyclist that focuses on velocity instead, check out my video on cycling aerodynamics.) When a car drives close behind a cyclist, it’s essentially pushing air ahead of it and into the cyclist’s wake. This actually reduces the difference in pressure between the cyclist’s front and back sides, thereby reducing his drag. Because cars are large, they have an oversized effect in this regard, but having a motorbike or another rider nearby also helps the lead cyclist aerodynamically.

    As for the Navier-Stokes equation – this effect isn’t one that you can really pin down to a single term since it’s a consequence of the flow overall. (Image credits: TU Eindhoven; K. Ramon)

  • Reader Question: Resonating Bottles

    Reader Question: Resonating Bottles

    Reader shoebill-san asks:

    why does it make that weird sound when i blow over a bottle? i did a science experiment in college where we looked at the resonance in a beaker at different water levels, is it like that? related?

    Blowing across the top of a bottle creates what’s called Helmholtz resonance, where air inside the neck of the bottle actually vibrates up and down, like you see in the animation above. The stream of air from your mouth creates low pressure just outside the bottle, pulling some of the air out. That air will tend to overshoot, ultimately causing pressure in the bottle neck to drop lower. That vacuum will pull air back into the bottle, at which point the low pressure your blowing supplies pulls it back out, and so on. The actual sound you hear comes from those puffs of moving air. In reality, they move too fast to see; the animation comes from a high-speed video, and I highly recommend watching the full vid.

    From your description, I’m not 100% sure what the experiment you did in college was, but I’m guessing it was some variation of the glass harp, where you rub a partially-filled glass and get an eerie sound that varies depending on how much water is in the glass. Like the bottle example above, that’s an example of resonance, but the two are different. In the bottle, it’s the air that’s resonating. For the glass harp, it’s the glass walls themselves that are resonating. The liquid inside just changes the pitch by slowing down the speed at which the glass’s walls vibrate. For a full and fantastic explanation of how that works, check out this video by Dan Quinn. (Image credit: N. Moore, source)

  • Reader Question: Rudders

    Reader Question: Rudders

    Reader le-mec writes:

    My question involves “fenestrated rudders”, a Chinese invention that
    involved cutting diamond-shaped holes in the rudders of ancient Chinese
    sailing ships (known as Junks). According to several articles (on the
    internet, ha ha), it reduces the amount of effort required to steer the
    ship at higher speeds with “no loss of function”. All I can find is
    anecdotal evidence and I’d like to know if these claims hold water or if
    they’re just steering us in the wrong direction.

    First off:

    image

    Now, I’m no expert on ships or sailing, but let’s talk rudders. Ships use rudders for steering. The rudder is completely submerged and turning it deflects water and creates a side force that helps steer a boat. In essence, it’s an underwater wing that generates lift in the side-to-side direction. Modern rudders even have the same shape as airfoils. That’s clearly not the case with the rudders of Chinese junks, but flat plates are a lot easier to make.

    There’s another key feature of the junk’s rudder, and that’s the way it’s mounted. The junk’s rudder attaches to the ship such that it rotates about its leading edge. This makes it an unbalanced rudder. More modern rudders are typically mounted so that they rotate around an axis that’s partway back on the rudder. This is called a balanced rudder; I’ve illustrated both below.

    image

    The advantage of the balanced rudder is that it’s easier to turn. You can see this for yourself without adding water into the equation. Imagine holding a big rectangular sheet. If you hold it by one edge and try to rotate it, you can do it, but it’s kind of difficult. If you instead hold it about a third of the way across, you’ll find rotating it easier. Once you have a fluid moving past, it will only magnify how hard it is to turn the rudder.

    So the Chinese junks had rudders that were harder to handle (by later ship-building standards) to begin with. By putting holes in the rudder, they equalized the pressure on either face of the rudder. That does make it easier to steer, since the helmsman is no longer fighting pressure differences across the rudder, but it would also reduce steering efficiency. It’s likely, however, given the slow speed of the junks, large rudder area, and their low hydrodynamic efficiency to begin with, that any drop in efficiency was negligible compared to the reduction in force necessary to steer.

    Since modern designs rely on foil shapes to generate pressure differences (and therefore side force) across the rudder, adding holes to them would be a bad idea. But back in the Song dynasty, the fenestrated rudder was major advance in nautical engineering!

    (Image credits: Chinese junk ship model – Premier Ship Models; Joffrey applauding – HBO; Rudder diagram – N. Sharp)

  • Reader Question: Lift

    Reader Question: Lift

    everyonelikespotatissallad asks:

    so, how is lift actually generated? i’ve been going through Anderson’s Introduction to Flight (6th Ed.) and while it offers the derivation of various equations very thoroughly, it barely touches on why lift is generated, or how camber contributes to the increase of C(L)

    This is a really good question to ask. There are a lot of different explanations for lift out there (and some of the common ones are incorrect). The main thing to know is that a difference in pressure across the wing–low pressure over the top and higher pressure below–creates the net upward force we call lift. It’s when you ask why there’s a pressure difference across the wing that explanations tend to start diverging. To be clear, aerodynamicists don’t disagree about what produces lift – we just tend to argue about which physical explanation (as opposed to just doing the math) makes the most sense. So here are a couple of options:

    Newton’s 3rd Law

    Newton’s third law states that for every action there is an equal and opposite reaction. If you look at flow over an airfoil, air approaching the airfoil is angled upward, and the air leaving the aifoil is angled downward. In order to change the direction of the air’s flow, the airfoil must have exerted a downward force on the air. By Newton’s third law, this means the air also exerted an upward force–lift–on the airfoil.

    The downward force a wing exerts on the air becomes especially obvious when you actually watch the air after a plane passes:

    Circulation

    This one can be harder to understand. Circulation is a quantity related to vorticity, and it has to do with how the direction of velocity changes around a closed curve. Circulation creates lift (which I discuss in some more detail here.) How does an airfoil create circulation, though? When an airfoil starts at rest, there is no vorticity and no circulation. As you see in the video above, as soon as the airfoil moves, it generates a starting vortex. In order for the total circulation to remain zero, this means that the airfoil must carry with it a second, oppositely rotating vortex. For an airfoil moving right to left, that carried vortex will spin clockwise, imparting a larger velocity to air flowing over the top of the wing and slowing down the air that moves under the wing. From Bernoulli’s principle, we know that faster moving air has a lower pressure, so this explains why the air pressure is lower over the top of the wing.

    Asymmetric Flow and Bernoulli’s Principle

    There are two basic types of airfoils – symmetric ones (like the one in the first picture above) and asymmetric, or cambered, airfoils (like the one in the image immediately above this). Symmetric airfoils only generate lift when at an angle of attack. Otherwise, the flow around them is symmetric and there’s no pressure difference and no lift. Cambered airfoils, by virtue of their asymmetry, can generate lift at zero angle of attack. Their variations in curvature cause air flowing around them to experience different forces, which in turn causes differing pressures along the top and the bottom of the airfoil surface. A fluid particle that travels over the upper surface encounters a large radius of curvature, which strongly accelerates the fluid and creates fast, low-pressure flow. Air moving across the bottom surface experiences a lesser curvature, does not accelerate as much, and, therefore, remains slower and at a higher pressure compared to the upper surface.

    (Image credit: M. Belisle/Wikimedia; National Geographic/BBC2; O. Cleynen/Wikimedia; video credit: J. Capecelatro et al.)

  • Reader Question: Submarines

    Reader Question: Submarines

    Reader elimik asks:

    Why do modern submarines have round bows instead of pointy ones, like the early WWII ones?

    Interestingly, there are more factors that affect this design choice than I originally thought! Perhaps the biggest factor, though, is propulsion. Although early submarines ran through several forms of propulsion from human power to steam, by World War II many subs were driven by diesel-power on the surface and relied on battery power when submerged. Power limitations meant that submarines of that era did most of their travel while at the surface, not underwater. As a result, the ships had better control and decreased drag with a pointed bow similar to that of a surface ship. It wasn’t until the advent of the nuclear-powered submarine that it became practical for submarines to spend most of their time submerged. Once fully-underwater travel was feasible (and, indeed, preferable), many subs transitioned to a blunter, rounded bow that’s more hydrodynamic underwater–and simultaneously more problematic control-wise when moving on the surface.

    Another factor separating WW-era submarines and modern subs is the depth to which they submerge. The deeper a submarine dives, the greater the pressure it must withstand. Rounded or cylindrical shapes make much better pressure vessels because they distribute pressure evenly around a surface. Historically, many subs have balanced control and hydrodynamics against pressure requirements by having two hulls, an outer one for cutting through surface waters and an inner cylindrical one that bears the brunt of the hydrostatic pressure. As we developed stronger materials, though, submarines have achieved greater depths. The German Type VII submarine, the most common U-boat of WWII, had a test depth of 230 m, whereas today’s Los-Angeles-class U.S. submarine can operate at 290 m. (Each 10 meters of depth adds about one atmosphere’s worth of pressure.) The combination of nuclear power for subsurface propulsion and stronger materials that allow deeper dives enables many modern submarines to have a single hull–the rounded hydrodynamic and pressure-resistant bow we commonly see.  (Image credits: U534 by P. Adams and USS George Washington by U.S. Navy)

  • Reader Question: Winglets

    Reader Question: Winglets

    Reader tvargo writes:

    First off… love your blog! I know very little about physics, but love reading about it. Could you potentially explain what the little upturned ends of wings do? looking on wikipedia is see this: “There are several types of wingtip devices, and although they function in different manners, the intended effect is always to reduce the aircraft’s drag by partial recovery of the tip vortex energy.” huh?

    Thanks! That’s a great question. Winglets are very common, especially on commercial airliners. To understand what they do, it’s helpful to first think about a winglet-less airplane wing. Each section of the wing produces lift. For a uniform, infinite wing, the lift produced at each spanwise location would be the same. In reality, though, wings are finite and wingtip vortices at their ends distort the flow. The vortices’ upward flow around the ends of the wing reduces the lift produced at the wing’s outermost sections, making the finite wing less efficient (though obviously more practical) than an infinite wing.

    Adding a winglet modifies the end conditions, both by redirecting the wingtip vortices away from the underside of the wing and by reducing the strength of the vortex. Both actions cause the winglet-equipped wing to produce more lift near the outboard ends than a wing without winglets.

    But why, you might ask, does the Wikipedia explanation talk about reducing drag? Since a finite wing produces less lift than an infinite one, finite wings must be flown at a higher angle of attack to produce equivalent lift. Increasing the angle of attack also increases drag on the wing. (If you’ve ever stuck a tilted hand out a car window at speed, then you’re familiar with this effect.) Because the winglet recovers some of the lift that would otherwise be lost, it allows the wing to be flown at a lower angle of attack, thereby reducing the drag. Thus, overall, adding winglets improves a wing’s efficiency. (Photo credit: C. Castro)

  • Reader Question: Fractals and Turbulence

    Reader Question: Fractals and Turbulence

    Reader 3d-time asks:

    Hi, there is a guy, at my college, who is doing a master’s degree thesis in turbulence. He says he uses fractals and computational methods. Can you explain how fractals can be used in fluid dynamics?

    That’s a good question! Fractals are a relatively recent mathematical development, and they have several features that make them an attractive tool, especially in the field of turbulence. Firstly, fractals, especially the Mandelbrot set shown above, demonstrate that great complexity can be generated out of simple rules or equations. Secondly, fractals have a feature known as self-similarity, meaning that they appear essentially the same regardless of scale. If you zoom in on the Mandelbrot set, you keep finding copy after copy of the same pattern. Nature, of course, doesn’t have this perfect infinite self-similarity; at some point things break down into atoms if you keep zooming in. But it is possible to have self-similarity across a large range of scales. This is where turbulence comes in. Take a look at the turbulent plume of the volcanic eruption in the photo above. Physically, it contains scales ranging from hundreds of meters to millimeters, and these scales are connected to one another by their motion and the energy being passed from one scale to another. There have been theories suggested to describe the relationship between these scales, but no one has yet found a theory truly capable of explaining turbulence as we observe it. Both the self-similarity and the complex nature of fractals suggest they could be useful tools in finally unraveling turbulence. In fact, Mandelbrot himself wrote several papers connecting the two concepts. Perhaps your friend will help find the next hints!  (Image credit: U.S. Geological Survey, Wikimedia)

  • Reader Question: What is Surface Tension?

    Reader Question: What is Surface Tension?

    Last week reader thesnazz asked:

    Is there a difference between surface tension and viscosity, or are they two manifestations of the same process and/or principles? If you know a given fluid’s surface tension, can you predict its viscosity, and vice versa?

    I’m tackling this one in parts, and you can click here to read about viscosity.

    Surface tension’s intermolecular origins are a bit clearer than those of viscosity. Essentially, within the interior of a water drop, you can imagine water molecules all hanging out with other water molecules. They tug on one another, but because they are surrounded on all sides by other water molecules, the net force of all these interactions on any molecule is zero. Not so at the surface of the drop. The surface is also called an interface; it’s a place where the fluid ends and something else–another fluid or perhaps a solid–begins. For a water molecule at that interface, the forces exerted by neighboring molecules are not balanced to zero. Instead, the imbalance causes the water molecules to be tugged inward. We call this effect surface tension.

    Because surface tension is an interfacial effect, it is not completely dependent on the fluid alone. For example, a drop of water sitting on a solid surface can take a variety of shapes depending on the properties of the solid (see also hydrophobicity) and the surrounding air as well as those of the water. This is only one of many manifestations of surface tension. Wikipedia has a pretty good overview of some others, if you’d like to learn more. Like viscosity, surface tension is usually measured rather than calculated from first principles.

    In the end, both surface tension and viscosity have molecular origins, but they are two very different and independent properties. Viscosity is inherent to a fluid, whereas surface tension depends on the fluid and its neighboring substance. Both quantities are more easily measured than calculated. Thanks again to thesnazz for a great question! As always, you can ask questions or submit post ideas here on Tumblr or via Twitter or email. (Image credit: Wikimedia)

  • Reader Question: What is Viscosity?

    Reader Question: What is Viscosity?

    Reader thesnazz asks:

    Is there a difference between surface tension and viscosity, or are they two manifestations of the same process and/or principles? If you know a given fluid’s surface tension, can you predict its viscosity, and vice versa?

    This is a good question! To answer it, let’s think about where surface tension and viscosity come from. Like many concepts in fluid dynamics, these quantities describe for a whole fluid the properties that arise from interactions between molecules.

    To prevent this becoming overly long, I’m going to tackle this over a couple posts. Today, I’ll talk about viscosity.

    One way to describe a fluid’s viscosity is as a measure of its resistance to deformation. Another way to think of it is how easily momentum is transmitted from one part of the fluid to another. The diagram above is the classic representation. A layer of fluid is sandwiched between two flat plates. If the top plate moves, friction requires that the fluid particles in contact with the plate get dragged along. This shears the fluid just below that and drags it along, but not quite as much. Those fluid particles do the same to their neighbors and so on down to the stationary second plate, where the fluid is at rest.

    Viscosity is the property that determines how much those neighboring fluid particles move; the more viscous the fluid, the more the neighboring bits of fluid resist getting pulled along. This is a property that’s inherent to a fluid. It comes from how the molecules of the fluid interact with one another, but there are no simple expressions to calculate the viscosity of a liquid or a gas from the individual interactions of its molecules. Instead we experimentally measure viscosity values and use empirical formulas to approximate how viscosity changes with temperature and other effects. (Image credit: Wikimedia)

  • Featured Video Play Icon

    Reader Question: Non-Coalescing Droplets

    Reader ancientavian asks:

    I’ve often noticed that, when water splashes (especially as with raindrops or other forms of spray), often it appears that small droplets of water skitter off on top of the larger surface before rejoining the main body. Is this an actual phenomenon, or an optical illusion? What causes it?

    That’s a great observation, and it’s a real-world example of some of the physics we’ve talked about before. When a drop hits a pool, it rebounds in a little pillar called a Worthington jet and often ejects a smaller droplet. This droplet, thanks to its lower inertia, can bounce off the surface. If we slow things way down and look closely at that drop, we’ll see that it can even sit briefly on the surface before all the air beneath it drains away and it coalesces with the pool below. But that kind of coalescence cascade typically happens in microseconds, far too fast for the human eye.

    But it is possible outside the lab to find instances where this effect lasts long enough for the eye to catch. Take a look at this video. Here Destin of Smarter Every Day captures some great footage of water droplets skittering across a pool. They last long enough to be visible to the naked eye. What’s happening here is the same as the situation we described before, except that the water surface is essentially vibrating! The impacts of all the multitude of droplets create ripples that undulate the water’s surface continuously. As a result, air gets injected beneath the droplets and they skate along above the surface for longer than they would if the water were still. (Video credit: SuperSloMoVideos)